题目内容

函数y=2^|x|的单调减区间是________．

（-∞，0]
分析：对于函数y=2^|x|，可去掉绝对值，讨论指数函数的单调性即可．
解答：∵当x＞0时，|x|=x，∴y=2^|x|=2^x是单调增函数；
当x≤0时，|x|=-x，∴y=2^|x|=2^-x= $\text{[math]}$ 是单调减函数；
∴函数y=2^|x|的单调减区间是（-∞，0]；
故答案为：（-∞，0]；
点评：本题通过绝对值考查了指数函数的单调性问题，是基础题．

练习册系列答案

微课堂百分大闯关系列答案

特级教师优化试卷系列答案

课程达标测试卷闯关100分系列答案

名师金考卷系列答案

新卷王期末冲刺100分系列答案

全能闯关100分系列答案

同步特训小博士系列答案

名师特攻冲刺100分系列答案

金榜一号同步单元全程达标测试AB卷系列答案

亮点激活3加1大试卷系列答案

相关题目

函数y=2^|x|的单调减区间是

已知函数f(x)= ax+blnx在x=1处有极值.

（1）求a,b的值;,科,网Z,X,X,K]

（2）判断函数y=f(x)的单调性并求出单调区间.

已知函数f(x)=a^x-a^-x(a＞0且a≠1)，
(1)判断函数y=f(x)的单调性；
(2)若f(1)=

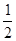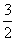，且g(x)=a^2x+a^-2x-2mf(x)在[1，+∞)上的最小值为-2，求实数m的值。

定义在R上的函数y=f(x)，f(0)≠0，当x＞0时，f(x)＞1，且对任意的a、b∈R，有f(a+b)=f(a)·f(b).

(1)求f(0)；

(2)证明对任意的x∈R，恒有f(x)＞0；

(3)判断函数y=f(x)的单调性.