题目内容
已知函数f(x)=ax-a-x(a>0且a≠1),
(1)判断函数y=f(x)的单调性;
(2)若f(1)=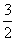 ,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求实数m的值。
,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求实数m的值。
(1)判断函数y=f(x)的单调性;
(2)若f(1)=
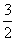 ,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求实数m的值。
,且g(x)=a2x+a-2x-2mf(x)在[1,+∞)上的最小值为-2,求实数m的值。解:(1)当a>1时,y=ax在R上单调递增,y=a-x= 在R上单调递减,
在R上单调递减,
所以,原函数在R上单调递增;
同理,当0<a<1时,原函数在R上单调递减;
(2) ,
,
∴ ,即2a2-3a-2=0,∴a=2或
,即2a2-3a-2=0,∴a=2或 (舍去),
(舍去),
∴ ,
,
令 ,
,
∵x≥1,∴ ,
,
∴g(t)=t2-2mt+2=(t-m)2+2-m2,
当 时,g(t)min=g(m)=2-m2=-2,
时,g(t)min=g(m)=2-m2=-2,
∴m=2或m=-2(舍去);
当 时,
时, ,
,
∴ (舍去);
(舍去);
综上可知m=2。
 在R上单调递减,
在R上单调递减,所以,原函数在R上单调递增;
同理,当0<a<1时,原函数在R上单调递减;
(2)
 ,
,∴
 ,即2a2-3a-2=0,∴a=2或
,即2a2-3a-2=0,∴a=2或 (舍去),
(舍去),∴
 ,
,令
 ,
,∵x≥1,∴
 ,
,∴g(t)=t2-2mt+2=(t-m)2+2-m2,
当
 时,g(t)min=g(m)=2-m2=-2,
时,g(t)min=g(m)=2-m2=-2,∴m=2或m=-2(舍去);
当
 时,
时, ,
,∴
 (舍去);
(舍去);综上可知m=2。

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |