题目内容
如图,扇形AOB的弧的中点为M,动点C,D分别在线段OA,OB上,且OC=BD.若OA=1,∠AOB=120°,则 的取值范围是 .
的取值范围是 .
【答案】分析:以OA为x轴,O为原点建立如图坐标系,得M( ,
, ).设C(1-m,0),则D(-
).设C(1-m,0),则D(- m,
m, m),可得向量
m),可得向量 和
和 的坐标,由向量数量积的坐标公式,得出
的坐标,由向量数量积的坐标公式,得出 •
• 关于m的二次函数表达式,再结合二次函数性质,可得
关于m的二次函数表达式,再结合二次函数性质,可得 的取值范围.
的取值范围.
解答:解:以OA为x轴,O为原点建立如图坐标系,则
∵半径OA=1,且∠AOB=120°,
∴弧AMB的中点M坐标为( ,
, )
)
求得BC方程为:y=- x,
x,
设C(1-m,0),则D(- m,
m, m),(0≤m≤1)
m),(0≤m≤1)
∴ =(
=( -m,-
-m,- ),
), =(-
=(- m-
m- ,
, m-
m- )
)
因此, •
• =(
=( -m)(-
-m)(- m-
m- )-
)- (
( m-
m- )
)
= m2-
m2- m+
m+ =
= (m-
(m- )2+
)2+
∴当m= 时,
时, •
• 有最小值为
有最小值为 ;当m=0或1时,
;当m=0或1时, •
• 有最小值为
有最小值为
故答案为:
点评:本题以扇形中的线段为例,求向量的数量积的取值范围,着重考查了二次函数的性质和平面向量数量积的运算性质等知识,属于中档题.
 ,
, ).设C(1-m,0),则D(-
).设C(1-m,0),则D(- m,
m, m),可得向量
m),可得向量 和
和 的坐标,由向量数量积的坐标公式,得出
的坐标,由向量数量积的坐标公式,得出 •
• 关于m的二次函数表达式,再结合二次函数性质,可得
关于m的二次函数表达式,再结合二次函数性质,可得 的取值范围.
的取值范围.解答:解:以OA为x轴,O为原点建立如图坐标系,则

∵半径OA=1,且∠AOB=120°,
∴弧AMB的中点M坐标为(
 ,
, )
)求得BC方程为:y=-
 x,
x,设C(1-m,0),则D(-
 m,
m, m),(0≤m≤1)
m),(0≤m≤1)∴
 =(
=( -m,-
-m,- ),
), =(-
=(- m-
m- ,
, m-
m- )
)因此,
 •
• =(
=( -m)(-
-m)(- m-
m- )-
)- (
( m-
m- )
)=
 m2-
m2- m+
m+ =
= (m-
(m- )2+
)2+
∴当m=
 时,
时, •
• 有最小值为
有最小值为 ;当m=0或1时,
;当m=0或1时, •
• 有最小值为
有最小值为
故答案为:

点评:本题以扇形中的线段为例,求向量的数量积的取值范围,着重考查了二次函数的性质和平面向量数量积的运算性质等知识,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
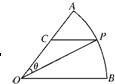 如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值. 如图,扇形AOB的弧的中点为M,动点C,D分别在线段OA,OB上,且OC=BD.若OA=1,∠AOB=120°,则
如图,扇形AOB的弧的中点为M,动点C,D分别在线段OA,OB上,且OC=BD.若OA=1,∠AOB=120°,则 的取值范围是 .
的取值范围是 .
 的取值范围是 .
的取值范围是 .