题目内容
若斜率为-2的直线l经过点(0,8),则直线l与两坐标轴围成的三角形面积为 .
考点:直线的截距式方程
专题:直线与圆
分析:求出直线方程,求出直线与x轴的交点,然后求解三角形的面积.
解答:
解:由题意可知所求直线方程为:y-8=-2x,当y=0时,x=4,直线在x轴上的截距为4,
则直线l与两坐标轴围成的三角形面积为:
×4×8=16.
故答案为:16.
则直线l与两坐标轴围成的三角形面积为:
| 1 |
| 2 |
故答案为:16.
点评:本题考查直线方程的应用,三角形的面积的求法,基本知识的考查.

练习册系列答案
相关题目
双曲线
-
=1上到定点(5,0)的距离是9的点的个数是( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、0个 | B、2个 | C、3个 | D、4个. |
已知函数f(x)是定义在R上的奇函数,且对任意x1、x2∈[1,a](a>1),当x1>x2时,都有f(x2)>f(x1)>0,则下列不等式不一定成立的是( )
| A、f(a)>f(0) | ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
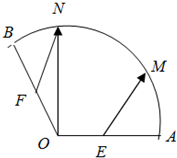 如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是
如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是