题目内容
1．在△ABC中，角A，B，C的对边分别为a，b，c，若B=45°，c=3$\sqrt{2}$，b=2$\sqrt{3}$，求角A．分析 由已知及正弦定理可得sinC=$\frac{csinB}{b}$=$\frac{\sqrt{3}}{2}$，利用范围C∈（0，π），可求C，根据三角形内角和定理即可求A的值．
解答 解：∵B=$\frac{π}{4}$，c=3$\sqrt{2}$，b=2$\sqrt{3}$，
∴由正弦定理可得：sinC=$\frac{csinB}{b}$=$\frac{3\sqrt{2}×\frac{\sqrt{2}}{2}}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$，
∵C∈（0，π），C=$\frac{π}{3}$或$\frac{2π}{3}$．
∴A=π-B-C=$\frac{5π}{12}$或$\frac{π}{12}$．
点评 本题主要考查了正弦定理，大边对大角，三角形内角和定理等知识的综合应用，考查了计算能力，属于基础题．
练习册系列答案
相关题目
如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE和CF的中点．
9．已知y=f（x）是定义在R上的偶函数，其对任意的x1，x2∈（-∞，0]，都使（x2-x1）[f（x2）-f（x1）]＜0成立，则当f（sinx）＞f（cosx）时，x的取值范围（ ）
| A． | （2kπ-$\frac{π}{4}$，2kπ+$\frac{π}{4}$），k∈Z | B． | （kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$），k∈Z | ||
| C． | （2kπ+$\frac{π}{4}$，2kπ+$\frac{3π}{4}$），k∈Z | D． | （kπ+$\frac{π}{4}$，kπ+$\frac{3π}{4}$），k∈Z |
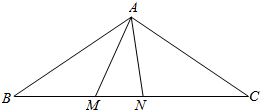如图，在等腰△ABC中，∠BAC=120°，AB=$\sqrt{3}$，点M在线段BC上．