题目内容
曲线y2=x在点P(| 1 |
| 4 |
| 1 |
| 2 |
分析:根据P点的坐标得到P为第一象限的点,所以得到y=
,然后求出y′,把x=
代入y′求得切线的斜率,根据P点坐标和斜率写出切线的方程即可.
| x |
| 1 |
| 4 |
解答:解:因为P点在第一象限,由曲线y2=x即y=
,所以y′=
,把x=
代入y′求得切线的斜率k=1,
则曲线在P点的切线方程为y-
=x-
即x-y+
=0
故答案为:x-y+
=0
| x |
| 1 | ||
2
|
| 1 |
| 4 |
则曲线在P点的切线方程为y-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:x-y+
| 1 |
| 4 |
点评:此题的突破点是由P点是第一象限的点可得y=
,要求学生会利用导数求曲线在某点切线的斜率以及会根据斜率和切点写出切线的方程.
| x |

练习册系列答案
相关题目
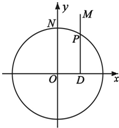 如图:⊙O方程为x2+y2=4,点P在圆上,点D在x轴上,点M在DP延长线上,⊙O交y轴于点N,
如图:⊙O方程为x2+y2=4,点P在圆上,点D在x轴上,点M在DP延长线上,⊙O交y轴于点N,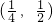 处的切线方程为 ________
处的切线方程为 ________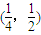 处的切线方程为
处的切线方程为