题目内容
18.满足a=4,b=3和A=45°的△ABC的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 不确定 |
分析 由已知及正弦定理可求得sinB的值,利用大边对大角可得满足条件的角B为锐角,可得满足条件的△ABC的个数只有1个.
解答 解:∵a=4,b=3和A=45°,
∴由正弦定理可求得sinB=$\frac{b•sinA}{a}$=$\frac{3\sqrt{2}}{8}$,
又∵a>b,可得:A>B,即满足条件的角B为锐角,
∴△ABC的个数只有1个.
故选:B.
点评 本题主要考查了大边对大角,正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
6.若存在两个正实数m、n,使得等式a(lnn-lnm)(4em-2n)=3m成立(其中e为自然对数的底数),则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,$\frac{3}{2e}$] | C. | [$\frac{3}{2e}$,+∞) | D. | (-∞,0)∪[$\frac{3}{2e}$,+∞) |
3.sin 15° sin 30° sin 75° 的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | -$\frac{1}{8}$ |
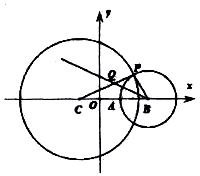 如图,在平面直角坐标系xoy中,已知圆C:(x+1)2+y2=16,点A(1,0),点B(a,0)(|a|>3),以B为圆心,|BA|的半径作圆,交圆C于点P,且的∠PBA的平分线次线段CP于点Q.
如图,在平面直角坐标系xoy中,已知圆C:(x+1)2+y2=16,点A(1,0),点B(a,0)(|a|>3),以B为圆心,|BA|的半径作圆,交圆C于点P,且的∠PBA的平分线次线段CP于点Q. 执行如图所示的程序框图,若输出的S=$\frac{15}{16}$,则输入的整数P的值为( )
执行如图所示的程序框图,若输出的S=$\frac{15}{16}$,则输入的整数P的值为( )