题目内容
一个多面体的直观图和三视图如下:(其中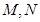 分别是
分别是 中点)
中点)

(1)求证: 平面
平面 ;
;
(2)求多面体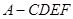 的体积.
的体积.
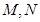 分别是
分别是 中点)
中点)
(1)求证:
 平面
平面 ;
;(2)求多面体
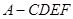 的体积.
的体积.(1) 取 中点
中点 ,连
,连 ,由
,由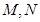 分别是
分别是 中点,可设:
中点,可设: , ∴面
, ∴面 面
面 ∴
∴ 面
面 (2)
(2)
 中点
中点 ,连
,连 ,由
,由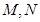 分别是
分别是 中点,可设:
中点,可设: , ∴面
, ∴面 面
面 ∴
∴ 面
面 (2)
(2)
试题分析:(1)由三视图知,该多面体是底面为直角三角形的直三棱柱,且
 ,
, ,∴
,∴ . ---2分
. ---2分取
 中点
中点 ,连
,连 ,由
,由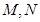 分别是
分别是 中点,可设:
中点,可设: ,
,∴面
 面
面 ∴
∴ 面
面 … ---8分
… ---8分(2)作
 于
于 ,由于三棱柱
,由于三棱柱 为直三棱柱
为直三棱柱 ∴
 面
面 ,
,且
 ∴
∴ ,---12
,---12点评:本题的关键是先由三视图找到直观图中对应的边长及边的垂直关系

练习册系列答案
相关题目
 中,棱长
中,棱长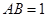 ,
, 、
、 分别为
分别为 、
、 的中点,
的中点, 、
、 是
是 、
、 的中点,
的中点,
 //平面
//平面 ;
; 到平面
到平面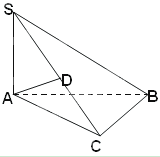

 .(
.( )
)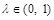 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF; ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的 中,
中, ,
,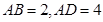 将
将 沿
沿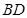 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面

 ;
;  的侧面积.
的侧面积.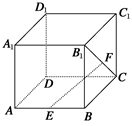
 β,给出四个命题:( )
β,给出四个命题:( )