题目内容
(本小题满分14分)
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.

(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足 .(
.( )
)
①求证:对于任意的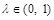 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;
②是否存在 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的 值;若不存在,说明理由.
值;若不存在,说明理由.
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.

(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足
 .(
.( )
)①求证:对于任意的
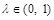 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;②是否存在
 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的 值;若不存在,说明理由.
值;若不存在,说明理由.(1)∵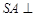 平面
平面 ∴
∴ ∴
∴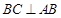 ∴
∴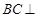 平面
平面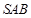 ∴平面
∴平面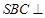 平面
平面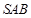 (2)①
(2)① ∴
∴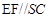
 SC∥平面AEF②
SC∥平面AEF②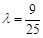
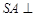 平面
平面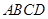 ∴
∴ ∴
∴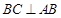 ∴
∴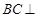 平面
平面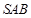 ∴平面
∴平面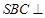 平面
平面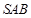 (2)①
(2)① ∴
∴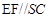
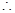 SC∥平面AEF②
SC∥平面AEF②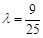
试题分析:(Ⅰ)∵
 平面
平面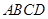 ,
,∴
 ……………1分
……………1分∵底面
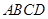 为直角梯形,
为直角梯形,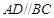 ,
,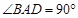 ,
,∴
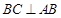 ……………2分
……………2分∵
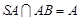
∴
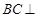 平面
平面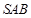 …………3分
…………3分∵
 平面
平面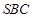
∴平面
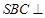 平面
平面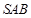 …………4分
…………4分(Ⅱ)(ⅰ)∵
 ,∴
,∴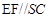 ………5分
………5分∵
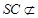 平面
平面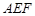 ,
, 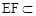 平面
平面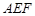 ,………6分
,………6分∴对于任意的
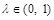 ,恒有SC∥平面AEF………7分
,恒有SC∥平面AEF………7分(ⅱ)存在
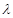 ,使得
,使得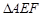 为直角三角形. ………8分
为直角三角形. ………8分若
 ,即
,即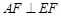
由(Ⅰ)知,
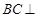 平面
平面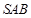 ,∵
,∵ 平面
平面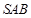 ,∴
,∴ 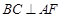 ,
,∵
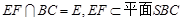 ,
,∴
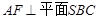 ,
,∴
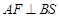 ,
,在
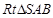 中,
中, ,
,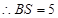 ,
,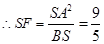 ,
,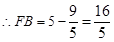 ,
,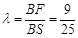 . ………10分
. ………10分②若
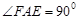 ,即
,即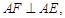 由①知,
由①知,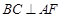 ,
, 平面
平面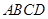 ,∴
,∴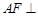 平面
平面 ,
,又因
 平面
平面 ,这与过一点有且只有一条直线与已知平面垂直相矛盾,
,这与过一点有且只有一条直线与已知平面垂直相矛盾,∴
 . ………12分
. ………12分③若
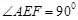 ,即
,即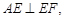 由(ⅰ)知,
由(ⅰ)知,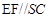 ,∴
,∴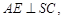
又∵
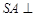 平面
平面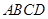 ,
,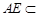 平面
平面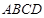 ,
,∴
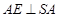 ,
,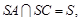 ∴
∴ 平面
平面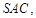
∴

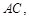 这与
这与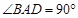 相矛盾,故
相矛盾,故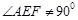
综上,当且仅当
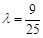 ,使得
,使得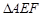 为直角三角形. ……… 14分
为直角三角形. ……… 14分点评:第二小题②采用空间向量求解比较简单

练习册系列答案
相关题目
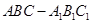 中,
中,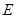 、
、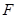 分别是
分别是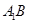 、
、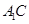 的中点,点
的中点,点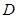 在
在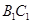 上,
上,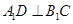 。
。
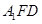
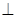 平面
平面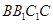
 中,
中,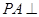 底面
底面 ,
, ,
, ,
,
 ,
, 是
是 的中点.
的中点. ;
; 平面
平面 ;
; 的正切值.
的正切值.
 中,
中,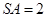 ,
, 的中点分别为
的中点分别为 ,且
,且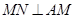 ,则正三棱锥
,则正三棱锥

 分别是
分别是 中点)
中点)
 平面
平面 ;
; 的体积.
的体积.