题目内容
求适合下列条件的直线方程:
(1)经过点P(3,2),且在两坐标轴上的截距相等;
(2)过点A(-1,-3),斜率是直线y=3x的斜率的- .
.
(3)过点A(1,-1)与已知直线l1:2x+y-6=0相交于B点,且 |AB|=5.
解 (1)法一 设直线l在x,y轴上的截距均为a,若a=0,即l过点(0,0)和(3,2),
∴l的方程为y=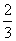 x,即2x-3y=0.
x,即2x-3y=0.
若a≠0,则设l的方程为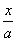 +
+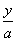 =1,
=1,
∵l过点(3,2),∴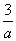 +
+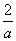 =1,
=1,
∴a=5,∴l的方程为x+y-5=0,
综上可知,直线l的方程为2x-3y=0或x+y-5=0.
法二 由题意,所求直线的斜率k存在且k≠0,
设直线方程为y-2=k(x-3),
令y=0,得x=3-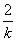 ,令x=0,得y=2-3k,
,令x=0,得y=2-3k,
由已知3-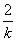 =2-3k,
=2-3k,
解得k=-1或k=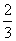 ,
,
∴直线l的方程为y-2=-(x-3)或y-2=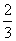 (x-3),
(x-3),
即x+y-5=0或2x-3y=0.
(2)设所求直线的斜率为k,依题意
k=- ×3=-
×3=- .
.
又直线经过点A(-1,-3),
因此所求直线方程为y+3=- (x+1),
(x+1),
即3x+4y+15=0.
(3)过点A(1,-1)与y轴平行的直线为x=1.
解方程组
求得B点坐标为(1,4),此时|AB|=5,
即x=1为所求.
设过A(1,-1)且与y轴不平行的直线为y+1=k(x-1),
解方程组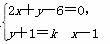
得两直线交点为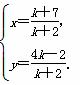
(k≠-2,否则与已知直线平行)
则B点坐标为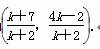 .
.
由已知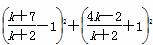 =52,
=52,
解得k=- ,∴y+1=-
,∴y+1=- (x-1),即3x+4y+1=0.
(x-1),即3x+4y+1=0.
综上可知,所求直线的方程为x=1或3x+4y+1=0.

练习册系列答案
相关题目
 的正方形
的正方形 沿
沿 轴滚动,点
轴滚动,点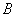 恰好经过原点.设顶点
恰好经过原点.设顶点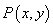 的轨迹方程是
的轨迹方程是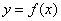 ,则对函数
,则对函数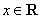 ,都有
,都有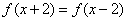 ;③函数
;③函数 上单调递减;④
上单调递减;④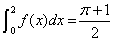 .其中判断正确的序号是 .
.其中判断正确的序号是 .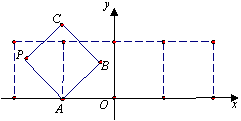
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, 是等差数列,且
是等差数列,且 ,则
,则 的值( )
的值( ) x+
x+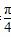 ,则直线l:ax-by+c=0的倾斜角为( )
,则直线l:ax-by+c=0的倾斜角为( ) 且被圆x2+y2=25截得的弦长是8,则该直线的方程为 ( ).
且被圆x2+y2=25截得的弦长是8,则该直线的方程为 ( ).
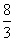 D.
D.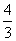
 表示三条不同的直线,
表示三条不同的直线, 表示两个不同的平面,则下列说法正确的是( )
表示两个不同的平面,则下列说法正确的是( ) ∥
∥ ,
, ,则
,则
 ,则
,则
 ,则
,则
 ,
, ,则
,则