题目内容
作出下列函数的图象并求出其值域．
（1）y=
；
（2）y=-x2+2x，x∈[-2，2]；
（3）y=|x+1|．
（1）y=
|
（2）y=-x2+2x，x∈[-2，2]；
（3）y=|x+1|．
考点：函数的图象,函数的值域
专题：数形结合法,函数的性质及应用
分析：列表，描点，连线，可得函数的图象，根据图象，求出其值域．
解答：
解（1）列表：
当0＜x＜1时，函数图象是双曲线y=
的一部分；
当x≥1时，函数图象为直线y=x的一部分，所以函数图象如图（1）所示，
由图（1），可得函数的值域是[1，+∞）．
（2）y=-x2+2x=1-（x-1）2，x∈[-2，2]．
列表：
画图象，图象是抛物线y=-x2+2x在-2≤x≤2之间的部分如图（2）所示．
由图（2），可得函数的值域是[-8，1]．
（3）当x+1≥0，
即x≥-1时，y=x+1；
当x+1＜0，即x＜-1时，y=-x-1．
作该分段函数图象如图（3）．
由图（3），可得函数的值域是[0，+∞）．
| x | … |
|
| 1 | 2 | 3 | … | ||||
| y | … | 4 | 2 | 1 | 2 | 3 | … |
| 1 |
| x |
当x≥1时，函数图象为直线y=x的一部分，所以函数图象如图（1）所示，
由图（1），可得函数的值域是[1，+∞）．
（2）y=-x2+2x=1-（x-1）2，x∈[-2，2]．
列表：
| x | -2 | -1 | 0 | 1 | 2 |
| y | -8 | -3 | 0 | 1 | 0 |
画图象，图象是抛物线y=-x2+2x在-2≤x≤2之间的部分如图（2）所示．
由图（2），可得函数的值域是[-8，1]．
（3）当x+1≥0，
即x≥-1时，y=x+1；
当x+1＜0，即x＜-1时，y=-x-1．
作该分段函数图象如图（3）．
由图（3），可得函数的值域是[0，+∞）．
点评：本题考查函数的图象并求出其值域，考查数形结合的数学思想，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，∠BAD=90°，PA=AD=AB=2BC，M是PC的中点．
省少年篮球队要从甲、乙两所体校选拔队员．现将这两所体校共20名学生的身高绘制成如下茎叶图（单位：cm）：若身高在180cm以上（包括180cm）定义为“高个子”，身高在180cm以下（不包括180cm）定义为“非高个子”．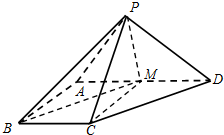
如图，四棱锥P-ABCD中，AB⊥AD，AD∥BC，AD=2，AB=BC=1，PA=PD=