题目内容

已知a、b不共线.

（1）实数x、y满足等式3xa+(10-y)b=(4y+7)a+2xb,求出x、y的值；

（2）把满足3x-2y=a,-4x+3y=b的向量x、y用a、b表示出来.

分析：由于a、b不共线，故（1）式成立时，需满足等式左右a、b的系数相等，即3x=4y+7,10-y=2x.解方程组即得x、y.第（2）题实际上是解两个向量方程构成的方程组，其中x、y为未知向量，a、b为已知向量.

解：（1）∵a、b为不共线向量，要使等式3xa+(10-y)b=(4y+7)a+2xb成立，则有

解得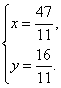

(2)

①×4+②×3得y=4a+3b.③

再将③代入①中得x=3a+2b.

∴

练习册系列答案
相关题目
已知
a
和
b
不共线，
OA
=p
a
，
OB
=q
b
（实数p≠0，q≠0），若点C在直线AB上，且
OC
=x
a
+y
b
（x，y是实数），则
x
p
+
y
q
=
1
1
．
下列命题错误的是（　　）
下列命题中，错误的命题是
④
④
．
①在四边形ABCD中，若
AC
=
AB
+
AD
，则ABCD为平行四边形
②已知
a
，
b
，
a
+
b
为非零向量，且a+b平分a与b的夹角，则|a|=|b|
③已知a与b不共线，则a+b与a-b不共线
④对实数λ1，λ2，λ3，则三向量λ1λ2，λ2b-λ3c，λ3c-λ1a不一定在同一平面上．
已知
a
，
b
不共线，且
a
•
b
≠0，若
c
=
a
-
a
•
a
a
•
b
b
，则
a
与
c
的夹角
90°
90°
．
已知
a
与
b
不共线，
p
=2
a
-3
b
，
q
=-
a
+5
b
，x
p
+y
q
=2
a
-
b
，则x=
 
，y=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网