题目内容
10.函数f(x)=ax3+(a-1)x2-x+2(0≤x≤1)在x=1处取得最小值,则实数a的取值范围是( )| A. | a≤0 | B. | 0$≤a≤\frac{3}{5}$ | C. | a≤$\frac{3}{5}$ | D. | a≤1 |
分析 求出函数的导数,通过讨论a的范围,通过函数的最小值是f(1),得到a的范围即可.
解答 解:f′(x)=3ax2+2(a-1)x-1,x∈[0,1],
a=0时,f′(x)=-2x-1<0,
f(x)在[0,1]递减,f(x)min=f(1)符合题意;
a≠0时,△=4(a2+a+1)>0,
x1=$\frac{1-a-\sqrt{{a}^{2}+a+1}}{3a}$,x2=$\frac{1-a+\sqrt{{a}^{2}+a+1}}{3a}$,
a>0时,若f(x)在x=1处取最小值,
只需x1≤0且x2≥1,解得:0<a≤$\frac{3}{5}$,
a<0时,若f(x)在x=1处取最小值,
只需x1≥1或x2≤0,解得:a<0;
综上:a≤$\frac{3}{5}$;
故选:C.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及二次函数的性质,是一道中档题.

练习册系列答案
相关题目
20.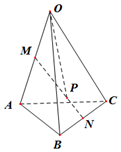 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |
5.关于x的方程xlnx-kx+1=0在区间[$\frac{1}{e}$,e]上有两个不等实根,则实数k的取值范围是( )
| A. | (1,1+$\frac{1}{e}$] | B. | (1,e-1] | C. | [1+$\frac{1}{e}$,e-1] | D. | (1,+∞) |
19.已知实数x、y满足不等式组$\left\{\begin{array}{l}y≥1\\ x-y≥0\\ x+2y-6≤0\end{array}\right.$时,目标函数z=2x+y的最大值为( )
| A. | 3 | B. | 6 | C. | 8 | D. | 9 |
20. 函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Acosωx的图象,只需将函数y=f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Acosωx的图象,只需将函数y=f(x)的图象( )
 函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Acosωx的图象,只需将函数y=f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Acosωx的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{2π}{3}$个单位长度 | B. | 向左平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{2π}{3}$个单位长度 | D. | 向右平移$\frac{π}{3}$个单位长度 |
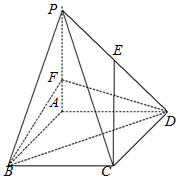 如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.
如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.