题目内容
(本题满分13分) 已知函数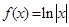
 ,函数
,函数
(I)当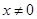 时,求函数
时,求函数 的表达式;
的表达式;
(II)若 ,且函数
,且函数 在
在 上的最小值是2 ,求
上的最小值是2 ,求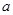 的值;
的值;
(III)对于(II)中所求的a值,若函数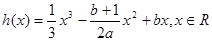 ,恰有三个零点,求b的取值范围。
,恰有三个零点,求b的取值范围。
【答案】
(Ⅰ)当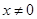 时,函数
时,函数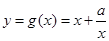 . (II)1;
. (II)1;
(III) 。
。
【解析】本试题主要是考查了导数在研究函数中的运用。利用导数求解最值和方程的解,以及解析式的求解的综合运用。
(1)∵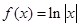 ,去掉绝对值然后分情况求解导数得到结论。
,去掉绝对值然后分情况求解导数得到结论。
∴当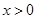 时,
时, ;
当
;
当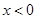 时,
时,
∴当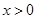 时,
时, ;
当
;
当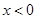 时,
时,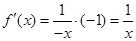 .
.
∴当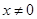 时,函数
时,函数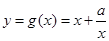 .
.
(2)由⑴知当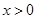 时,
时,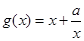 ,
,
∴当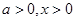 时,
时,  当且仅当
当且仅当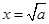 时取等号.由
时取等号.由 ,得a=1 (8分)
,得a=1 (8分)
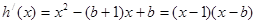
分析导数的运用。
(3)构造函数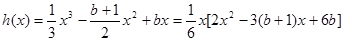
所以,方程
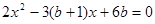 ,有两个不等实根,且不含零根。等价转化后得到。
,有两个不等实根,且不含零根。等价转化后得到。
解: (Ⅰ)∵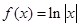 ,
,
∴当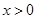 时,
时, ;
当
;
当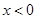 时,
时,
∴当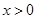 时,
时, ;
当
;
当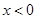 时,
时,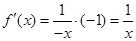 .
.
∴当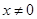 时,函数
时,函数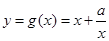 . (4分)
. (4分)
(Ⅱ)∵由⑴知当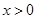 时,
时,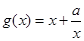 ,
,
∴当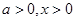 时,
时,  当且仅当
当且仅当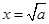 时取等号.由
时取等号.由 ,得a=1 (8分)
,得a=1 (8分)
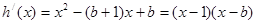
令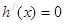 ,得
,得 或x=b
或x=b
(1)
若b>1,则当0<x<1时,
 ,当1<x<b,时
,当1<x<b,时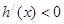 ,当x>b时,
,当x>b时, ;
;
(2)
若b<1,且b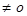 则当0<x<b时,
则当0<x<b时, ,当b<x<1时,
,当b<x<1时,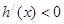 ,当x>1时,
,当x>1时,
所以函数h(x)有三个零点的充要条件为 或
或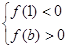 解得
解得 或
或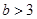
综合: (13分)
(13分)
另解: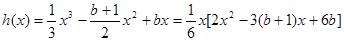
所以,方程
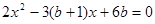 ,有两个不等实根,且不含零根
,有两个不等实根,且不含零根
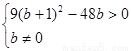 解得:
解得: (13分)
(13分)

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.