题目内容

已知：在△ABC中，a，b，c分别是∠A，∠B，∠C的对边．
求证： $数学公式$ ．

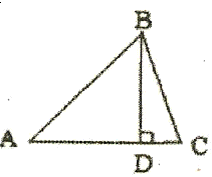证法一：如图，在△ABC中，过点B作BD⊥AC，垂足为D，
∵BD=BD，
∴ABsinA=BCsinC，…（2分）
即csinA=asinC? $\text{[math]}$ = $\text{[math]}$ ，…（4分）
同理可证 $\text{[math]}$ = $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．…（5分）
证法二：
如图，在△ABC中，过点B作BD⊥AC，垂足为D
sin∠ABC=sin[180°-（A+C）]=sin（A+C）
=sinAcosC+cosAsinC…（2分）
= $\text{[math]}$ • $\text{[math]}$ + $\text{[math]}$ • $\text{[math]}$
= $\text{[math]}$
= $\text{[math]}$
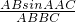
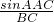
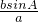= $\text{[math]}$ ，…（4分）
∴asinB=bsinA，
∴ $\text{[math]}$ = $\text{[math]}$ ，
同理可证 $\text{[math]}$ = $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．…（5分）
分析：证法一：如图，在△ABC中，过点B作BD⊥AC，垂足为D，利用ABsinA=BCsinC即可证得 $\text{[math]}$ = $\text{[math]}$ ，同理可证 $\text{[math]}$ = $\text{[math]}$ ．
证法二：作图同上，利用sin∠ABC=sin（A+C）=sinAcosC+cosAsinC，将sinA、cosC、cosA、sinC分别用线段之比代换整理即可得sin∠ABC= 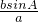$\text{[math]}$ ，同理可证 $\text{[math]}$ = $\text{[math]}$ ．
点评：本题考查正弦定理的证明，考查三角函数的诱导公式及三角函数式的综合应用，考查推理证明能力，属于中档题．