Question

已知：在△ABC中，AB=c，BC=a，AC=b，AB上的中线CD=m，求证：a²+b²=

1

2

c²+2m²．

Answer 1

分析：法一：在△ABC中，要证：a²+b²=

1

2

c²+2m²成立，可以用（向量法），即

BC

=

BD

+ 

DC

，

AC

=

AD

+

DC

，两式平方相加可得结论；
法二：根据余弦定理，a2=(

1

2

c)2+m2-2•

1

2

c•m•cos∠BDC，b2=(

1

2

c)2+m2-2•

1

2

c•m•cos∠ADC，两式相加即得结论．

解答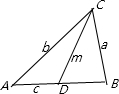：证明：法一：如图所示（向量法），在△ABC中，
∵

BC

=

BD

+ 

DC

 ①，

AC

=

AD

+

DC

 ②，
且|

BC

|=a，|

AC

|=b，|

AD

|=|

BD

|=

1

2

c，|

DC

|=m；
①②两式平方相加，可得：a²+b²=

1

2

c²+2m²+2（

BD

•

DC

+

AD

•

DC

）；
∵

BD

•

DC

+

AD

•

DC

=|

BD

||

DC

|•cos∠BDC+|

AD

||

DC

|cos∠CDA=

1

2

c•m•cos∠BDC+

1

2

c•m•cos（π-∠BDC）=0；
∴a²+b²=

1

2

c²+2m²．即证．
法二：（余弦定理法）在△ABC中，由余弦定理，得a2=(

1

2

c)2+m2-2•

1

2

c•m•cos∠BDC，b2=(

1

2

c)2+m2-2•

1

2

c•m•cos∠ADC，两式相加，得
a2+b2=

1

2

c2+2m2-cm•cos∠BDC-cm•cos（π-∠BDC）=

1

2

c²+2m²；即证．

点评：本题在三角形中考查了平面向量的线性表示和基本的运算，属于基础题；本题也可以应用余弦定理，得出证明，解题思路比较多．