题目内容
11．若直线m、n的方向向量分别为$\overrightarrow{a}$，$\overrightarrow{b}$，则“m∥n“是“$\overrightarrow{a}$∥$\overrightarrow{b}$“的（ ）| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充分必要条件 | D． | 既非充分又非必要条件 |
分析 由直线的平行关系和充要条件的判定可得．
解答 解：由直线m∥n可得其方向向量分别为$\overrightarrow{a}$∥$\overrightarrow{b}$，
而当$\overrightarrow{a}$∥$\overrightarrow{b}$时，直线m和n可能重合，即不能推出平行，
故选“m∥n“是“$\overrightarrow{a}$∥$\overrightarrow{b}$“的充分不必要条件．
故选：A
点评 本题考查充要条件的判定，涉及直线平行关系与方向向量的关系，属基础题．
练习册系列答案
相关题目
6．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别F1（-c，0），F2（c，0），若双曲线上存在点P满足$\frac{a}{sin∠PF{{\;}_{1}F}_{2}}$=$\frac{c}{sin∠P{F}_{2}{F}_{1}}$1，则该曲线的离心率的取值范围为（ ）
| A． | （1，$\sqrt{2}$+1） | B． | （1，$\sqrt{3}$） | C． | （$\sqrt{3}$，+∞） | D． | （$\sqrt{2}$+1，+∞） |
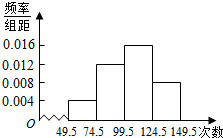为了调查学生的课外阅读情况，在某班级对全体学生每天阅读时间（单位：分钟）进行调查，将调查数据整理后，画出频率分布直方图如图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第三组的频数为20．
3．下列函数既是奇函数，又在区间[-1，1]上单调递增的是（ ）
| A． | y=sin2x | B． | y=-|x+1| | C． | y=ln$\frac{2+x}{2-x}$ | D． | y=$\frac{{a}^{x}+{a}^{-x}}{2}$ |
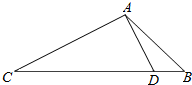如图△ABC中，已知点D在BC边上，且AD⊥AC，sin∠BAC=$\frac{{2\sqrt{2}}}{3}$，AB=3$\sqrt{2}$，BD=$\sqrt{3}$．