题目内容
已知0<α<
解析:∵![]() 是特殊角,由两角差的正弦三角函数式,知欲求sin(α-
是特殊角,由两角差的正弦三角函数式,知欲求sin(α-![]() )的值,只要能求得α的正、余弦即可,而题给条件是α的半角,∴解题的关键是将tan
)的值,只要能求得α的正、余弦即可,而题给条件是α的半角,∴解题的关键是将tan![]() +cot
+cot![]() “切割化弦”.
“切割化弦”.
∵tan![]() +cot
+cot![]()
=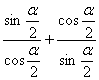
=![]() =
=![]() ,
,
∴sinα=![]() .
.
又∵0<α<![]() ,
,
∴cosα=![]() =
=![]() ,
,
从而sin(α-![]() )
)
=sinαcos![]() -cosαsin
-cosαsin![]()
=![]() ×
×![]() -
-![]() ×
×![]()
=![]() (4-3
(4-3![]() ).
).

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
题目内容
已知0<α<
解析:∵![]() 是特殊角,由两角差的正弦三角函数式,知欲求sin(α-
是特殊角,由两角差的正弦三角函数式,知欲求sin(α-![]() )的值,只要能求得α的正、余弦即可,而题给条件是α的半角,∴解题的关键是将tan
)的值,只要能求得α的正、余弦即可,而题给条件是α的半角,∴解题的关键是将tan![]() +cot
+cot![]() “切割化弦”.
“切割化弦”.
∵tan![]() +cot
+cot![]()
=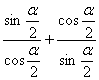
=![]() =
=![]() ,
,
∴sinα=![]() .
.
又∵0<α<![]() ,
,
∴cosα=![]() =
=![]() ,
,
从而sin(α-![]() )
)
=sinαcos![]() -cosαsin
-cosαsin![]()
=![]() ×
×![]() -
-![]() ×
×![]()
=![]() (4-3
(4-3![]() ).
).

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案