Question

如图，在直角梯形ABCD中，AB⊥AD，AD=DC=1，AB=3，动点P在以点C为圆心，且与直线BD相切的圆内运动，设

AP

=α

AD

+β

AB

（α，β∈R），则α+β的取值范围是（　　）

• A、（0，

  4

  3

  ]
• B、[

  4

  3

  ，

  5

  3

  ]
• C、（1，

  4

  3

  ）
• D、（1，

  5

  3

  ）

Answer 1

考点：向量在几何中的应用

专题：综合题,平面向量及应用

分析：建立直角坐标系，写出点的坐标，求出BD的方程，求出圆的方程；设出P的坐标，求出三个向量的坐标，将P的坐标用α，β表示，代入圆内方程求出范围．

解答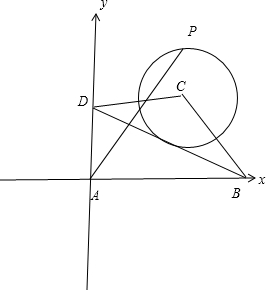： 解：以A为坐标原点，AB为x轴，DA为y轴建立平面直角坐标系，则A（0，0），D（0，1），C（1，1），B（3，0）
直线BD的方程为x+3y-3=0，C到BD的距离d=

10

10

∴以点C为圆心，且与直线BD相切的圆方程为（x-1）²+（y-1）²=

1

10

，
设P（x，y）则

AP

=（x，y），

AD

=（0，1），

AB

=（3，0）
∴（x，y）=（3β，α）
∴x=3β，y=α，
∵P在圆内
∴（3β-1）²+（α-1）²＜

1

10

，
解得1＜α+β＜

5

3

．
故选：D．

点评：通过建立直角坐标系将问题代数化、考查直线与圆相切的条件、考查向量的坐标公式．