题目内容

设正方体ABCD-A₁B₁C₁D₁的棱长为1，则点B到平面AB₁C的距离为________．

$\text{[math]}$
分析：根据点B到平面AB₁C的距离是正方体的体对角线的 $\text{[math]}$ ，而正方体的体对角线为 $\text{[math]}$ ，即可求出点B到平面AB₁C的距离；
解答：正方体的体对角线为 $\text{[math]}$
而点B到平面AB₁C的距离是正方体的体对角线的 $\text{[math]}$
∴点B到平面AB₁C的距离为 $\text{[math]}$ ；
故答案为： $\text{[math]}$ ．
点评：本题主要考查了点到平面的距离，同时考查了空间想象能力，计算推理能力，属于基础题．

练习册系列答案

寒假作业长江少年儿童出版社系列答案

熠光传媒寒假生活云南出版社系列答案

义务教育教科书寒假作业系列答案

学与练寒假生活系列答案

学与练快乐寒假系列答案

学新教辅寒假作业系列答案

期末加寒假系列答案

学生寒假实践手册系列答案

学期总复习状元成才路寒假系列答案

阳光假期学期总复习系列答案

相关题目

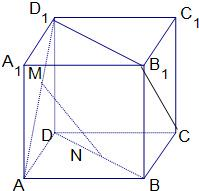如图ABCD-A₁B₁C₁D₁是正方体，M、N分别是线段AD₁和BD上的中点
（Ⅰ）证明：直线MN∥平面B₁D₁C；
（Ⅱ）设正方体ABCD-A₁B₁C₁D₁棱长为a，若以D为坐标原点，分别以DA，DC，DD₁所在的直线为x轴、y轴、z轴，建立空间直角坐标系，试写出B₁、M两点的坐标，并求线段B₁M的长．

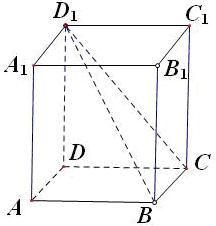设正方体ABCD-A₁B₁C₁D₁的棱长为1，则
（1）A点到CD₁的距离为

；
（2）A点到BD₁的距离为

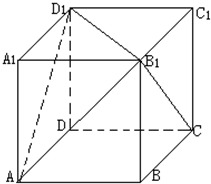（2006•丰台区二模）如图，设正方体ABCD-A₁B₁C₁D₁的棱长为1，则直线B₁C与平面AB₁D₁所成的角是（　　）

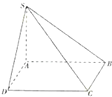（2011•许昌三模）已知四棱锥S-ABCD中，AB=BC=CD=DA=SA=2，底面ABCD是正方形，SD=SB=2

．
（I）在该四棱锥中，是否存在一条侧棱垂直于底面？如果存在，请给出证明；
（Ⅱ）用多少个这样的四棱锥可以拼成一个棱长为2的正方体ABCD-A₁B₁C₁D₁？说明你的结论．
（Ⅲ）在（Ⅱ）的条件下，设正方体ABCD-A₁B₁C₁D₁的棱BB₁的中点为N，棱DD₁的中点为M，求二面角A-MN-C的大小的余弦值．

如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F 分别是棱AA'，CC'的中点，过直线E、F的平面分别与棱BB′，DD′交于M、N，设BM=x，x∈[0，1]，给出以下四个命题：
①当且仅当x=0时，四边形MENF的周长最大；
②当且仅当x=

时，四边形MENF的面积最小；
③四棱锥C′-MENF的体积V=h（x）为常函数；
④正方体ABCD-A′B′C′D′被截面MENF平分成等体积的两个多面体．
以上命题中正确命题的个数（　　）