Question

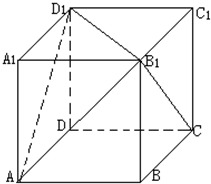（2006•丰台区二模）如图，设正方体ABCD-A₁B₁C₁D₁的棱长为1，则直线B₁C与平面AB₁D₁所成的角是（　　）

• A．

  π

  2

• B．arccos

  3

  3

• C．

  π

  4

• D．arccos

  3

  6

Answer 1

分析：根据线面角的定义先确定直线B₁C与平面AB₁D₁所成的角平面角，然后根据条件进行求值即可．

解答：解：以D为坐标原点，建立空间坐标系如图：
则A（1，0，0），D₁（0，0，1），B_{1（1，1，1）}，C（0，1，0）．
则

B1C

=(-1，0，-1)，

AD1

=(-1，0，1)，

AB1

=(0，1，1)，
设平面AB₁D₁的法向量为

n

=(x，y，z)，则由

n • AD1 =0 n • AB1 =0

，得

-x+z=0 y+z=0

，令z=1，则x=1，y=-1，即

n

=(1，-1，1)．
则

n

•

B1C

=(1，-1，1)•(-1，0，-1)=-1-1=-2，|

n

|=

3

，|

B1C

|=

2

．
所以设直线B₁C与平面AB₁D₁所成的角是θ，则sin?θ=|cos?(

π

2

-θ)|=

| n ? B1C |

| n || B1C |

=

2

2 × 3

=

2

3

，所以cosθ=

3

3

，
即θ=arccos

3

3

．
故选B．

点评：本题只有考查空间直线和平面所成角的求法，利用向量法是解决空间角的基本方法，考查学生的运算能力．