题目内容
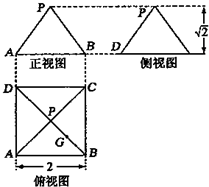 某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.(Ⅰ)根据三视图,画出该几何体的直观图;
(Ⅱ)在直观图中,①证明:PD∥面AGC;②证明:面PBD⊥AGC.
考点:直线与平面平行的判定,由三视图求面积、体积
专题:空间位置关系与距离
分析:(Ⅰ)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为
,由此可得该几何体的直观图.
(Ⅱ)①证明:在直观图中,设正方形ABCD的中心为O,利用三角形的中位线证明OG∥PD.再由直线和平面平行的判定定理证得 PD∥面AGC.
②正方形ABCD中,AC⊥BD.再由正四棱锥P-ABCD 的性质可得PO⊥平面ABCD,可得AC⊥平面PBD,可得AC⊥GO.再利用直线和平面垂直的判定定理得AC⊥面PBD,从而证得面PBD⊥平面AGC.
| 2 |
(Ⅱ)①证明:在直观图中,设正方形ABCD的中心为O,利用三角形的中位线证明OG∥PD.再由直线和平面平行的判定定理证得 PD∥面AGC.
②正方形ABCD中,AC⊥BD.再由正四棱锥P-ABCD 的性质可得PO⊥平面ABCD,可得AC⊥平面PBD,可得AC⊥GO.再利用直线和平面垂直的判定定理得AC⊥面PBD,从而证得面PBD⊥平面AGC.
解答:
 解:(Ⅰ)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为
解:(Ⅰ)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为
,
该几何体的直观图如图所示:
(Ⅱ),①证明:在直观图中,设正方形ABCD的中心为O,∵G是PB的中点,
∴OG是△PAD的中位线,故有OG∥PD.
而OG?面AGC,PD?面AGC,∴PD∥面AGC.
②证明:正方形ABCD中,AC⊥BD,再由正四棱锥P-ABCD 的性质可得PO⊥平面ABCD,而PO?平面PBD,
∴平面PBD⊥平面ABCD,且平面PBD∩平面ABCD=BD,∴AC⊥平面PBD.
而GO?平面PBD,∴AC⊥GO.
根据BD和GO是平面AGC内的两条相交直线,可得AC⊥面PBD.
由AC?平面AGC,可得面PBD⊥平面AGC.
 解:(Ⅰ)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为
解:(Ⅰ)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为| 2 |
该几何体的直观图如图所示:
(Ⅱ),①证明:在直观图中,设正方形ABCD的中心为O,∵G是PB的中点,
∴OG是△PAD的中位线,故有OG∥PD.
而OG?面AGC,PD?面AGC,∴PD∥面AGC.
②证明:正方形ABCD中,AC⊥BD,再由正四棱锥P-ABCD 的性质可得PO⊥平面ABCD,而PO?平面PBD,
∴平面PBD⊥平面ABCD,且平面PBD∩平面ABCD=BD,∴AC⊥平面PBD.
而GO?平面PBD,∴AC⊥GO.
根据BD和GO是平面AGC内的两条相交直线,可得AC⊥面PBD.
由AC?平面AGC,可得面PBD⊥平面AGC.
点评:本题主要考查三视图、直线和平面平行的判定定理、直线和平面垂直的判定定理、平面和平面垂直的判定定理的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为y1=5.06x-0.15x2和y2=2x,其中x为销售量(单位:辆),若该公司在这两地共销售15辆车,则能获得的最大利润为( )
| A、45.6万元 |
| B、45.606万元 |
| C、45.56万元 |
| D、45.51万元 |
a、b是不互相垂直的异面直线,α、β是分别过a、b的平面,则下列四种情况:
①α∥β;②α⊥β;③a∥β;④a⊥β,
其中可能出现的有( )
①α∥β;②α⊥β;③a∥β;④a⊥β,
其中可能出现的有( )
| A、1种 | B、2种 | C、3种 | D、4种 |