题目内容
某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为y1=5.06x-0.15x2和y2=2x,其中x为销售量(单位:辆),若该公司在这两地共销售15辆车,则能获得的最大利润为( )
| A、45.6万元 |
| B、45.606万元 |
| C、45.56万元 |
| D、45.51万元 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:根据条件建立函数关系,利用一元二次函数的性质即可得到结论.
解答:
解:设卖甲种品牌车x量,由题意可得利润y=5.06x-0.15x2+2(15-x)=-0.15x2+3.06x+30=-0.15(x-10.2)2+45.606.
根据二次函数性质和x∈N*,
可知当x=10时,获得最大利润L=-0.15×102+3.06×10+30=45.6万元,
故选:A
根据二次函数性质和x∈N*,
可知当x=10时,获得最大利润L=-0.15×102+3.06×10+30=45.6万元,
故选:A
点评:本题考查函数模型的构建,考查利用配方法求函数的最值,解题的关键是正确构建函数解析式

练习册系列答案
相关题目
与曲线
+
=1共焦点,而与曲线
-
=1共渐近线的双曲线方程为( )
| x2 |
| 24 |
| y2 |
| 49 |
| x2 |
| 36 |
| y2 |
| 64 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
、
、
是不共面的三个向量,则下列向量组能作为一个基底的是( )
| a |
| b |
| c |
A、2
| ||||||||||
B、2
| ||||||||||
C、
| ||||||||||
D、
|
已知A、B、C三点不共线,O为平面ABC外的一点,
=
+
+λ
,且P与A、B、C四点共面,则λ的值为( )
| OP |
| 1 |
| 5 |
| OA |
| 2 |
| 3 |
| OB |
| OC |
A、
| ||
B、
| ||
C、-
| ||
| D、不能确定 |
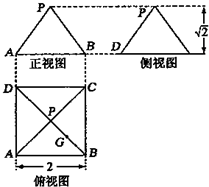 某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.