题目内容
设函数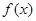 的定义域为
的定义域为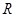 ,对任意的实数
,对任意的实数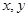 都有
都有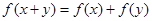 ;当
;当 时,
时,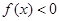 ,且
,且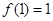 .(1)判断并证明
.(1)判断并证明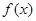 在
在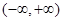 上的单调性;
上的单调性;
(2)若数列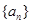 满足:
满足: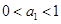 ,且
,且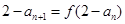 ,证明:对任意的
,证明:对任意的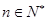 ,
,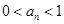
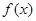 的定义域为
的定义域为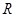 ,对任意的实数
,对任意的实数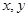 都有
都有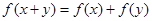 ;当
;当 时,
时,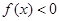 ,且
,且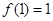 .(1)判断并证明
.(1)判断并证明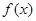 在
在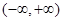 上的单调性;
上的单调性;(2)若数列
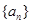 满足:
满足: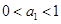 ,且
,且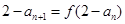 ,证明:对任意的
,证明:对任意的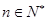 ,
,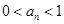
(1)单调递增(2) ,再利用
,再利用 .
.
 ,再利用
,再利用 .
.试题分析:(1)
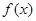 在
在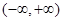 上单调递增,证明如下: 设任意
上单调递增,证明如下: 设任意
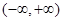 ,且
,且 ,∵
,∵ ,∴
,∴ ,∴
,∴


即
 ,∴
,∴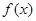 在
在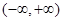 上单调递增.
上单调递增. (2)在
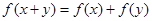 中,令
中,令 ,得
,得 .令
.令 ,
,得
 ,∴
,∴ .令
.令 ,得
,得 ,即
,即

下面用数学归纳法证明:
①当
 时,
时,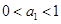 ,不等式成立;
,不等式成立;②假设当
 时,不等式成立,即
时,不等式成立,即 ,则∵
,则∵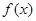 在
在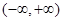 上单调递增,
上单调递增,∴
 ,∴
,∴ ,即当
,即当 时不等式也成立.
时不等式也成立.综上①②,由数学归纳法原理可知对任意的
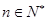 ,
,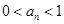
点评:本题考查函数的单调性,考查数学归纳法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
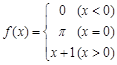 ,则
,则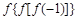 =( )
=( )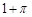
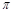
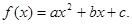
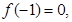 试判断函数
试判断函数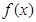 零点个数;
零点个数;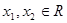 ,且
,且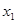 <
<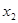 ,
,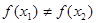 (
(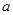 >0),试证明:
>0),试证明: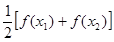 >
>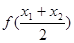 成立。
成立。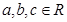 ,使
,使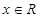 ,
,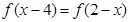 ,且
,且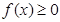 ②对任意的
②对任意的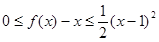 ?若存在,求出
?若存在,求出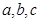 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。 是定义在
是定义在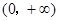 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记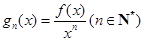 .若对定义域内的每一个
.若对定义域内的每一个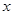 ,总有
,总有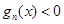 ,则称
,则称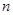 阶负函数 ”;若对定义域内的每一个
阶负函数 ”;若对定义域内的每一个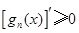 ,则称
,则称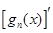 为函数
为函数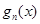 的导函数).
的导函数).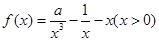 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数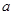 的取值范围;
的取值范围;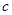 ,使得
,使得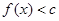 恒成立,试判断
恒成立,试判断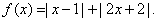
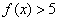 ;
;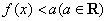 的解集为空集,求
的解集为空集,求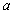 的取值范围.
的取值范围.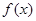 的图象恰好通过
的图象恰好通过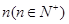 个整点,则称函数
个整点,则称函数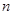 阶整点函数。有下列函数:
阶整点函数。有下列函数: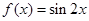 ; ②
; ②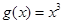 ③
③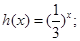 ④
④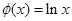 ,
,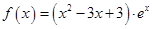 ,设
,设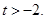
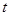 的取值范围,使得函数
的取值范围,使得函数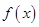 在
在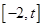 上为单调函数;
上为单调函数;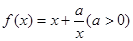 .
.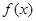 在定义域上的单调性;
在定义域上的单调性;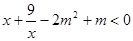 在
在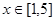 上恒成立时的实数
上恒成立时的实数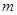 的取值范围?
的取值范围?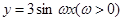 在区间
在区间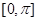 恰有2个零点,则
恰有2个零点,则 的取值范围是( )
的取值范围是( )