题目内容
函数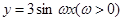 在区间
在区间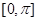 恰有2个零点,则
恰有2个零点,则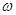 的取值范围是( )
的取值范围是( )
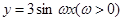 在区间
在区间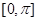 恰有2个零点,则
恰有2个零点,则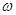 的取值范围是( )
的取值范围是( )A.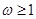 | B.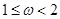 | C.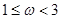 | D.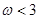 |
B
试题分析:要满足函数
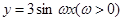 在区间
在区间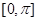 恰有2个零点,需
恰有2个零点,需 ,所以
,所以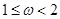 。
。点评:此题我们可以结合图像来分析,这个更形象,更直观。函数
 的周期公式为:
的周期公式为: ;函数
;函数 的周期公式为:
的周期公式为: 。注意两个函数周期公式的区别。
。注意两个函数周期公式的区别。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
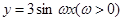 在区间
在区间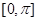 恰有2个零点,则
恰有2个零点,则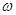 的取值范围是( )
的取值范围是( )A.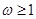 | B.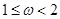 | C.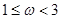 | D.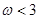 |
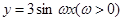 在区间
在区间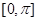 恰有2个零点,需
恰有2个零点,需 ,所以
,所以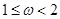 。
。 的周期公式为:
的周期公式为: ;函数
;函数 的周期公式为:
的周期公式为: 。注意两个函数周期公式的区别。
。注意两个函数周期公式的区别。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案