题目内容
如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= .
.

(Ⅰ)若M为PA中点,求证:AC∥平面MDE;
(Ⅱ)求平面PAD与PBC所成锐二面角的大小.
【答案】
(Ⅰ) 参考解析;(Ⅱ) 60°
【解析】
试题分析:(Ⅰ)直线与平面平行的判定定理是在平面内找一条直线与该直线平行,由于点M是PA的中点,联想到连结PC与ED它们的交点也是ED的中点,所以可得MN∥AC.从而可得结论.本小题通过已知的中点利用三角形的中位线定理得到平行是解题的突破口.
试题解析:(1)证明:连接PC,交DE与N,连接MN,
在△PAC中,∵M,N分别为两腰PA,PC的中点
∴MN∥AC, (2分)
又AC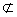 面MDE,MN?面MDE,
面MDE,MN?面MDE,
所以AC∥平面MDE. (4分)
(2)以D为空间坐标系的原点,分别以 DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系,
则P(0,0,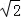 a),B(a,a,0),C(0,2a,0),
a),B(a,a,0),C(0,2a,0),
所以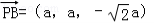 ,
,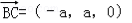 , (6分)
, (6分)
设平面PAD的单位法向量为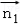 ,则可取
,则可取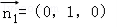 (7分)
(7分)
设面PBC的法向量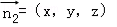 ,
,
则有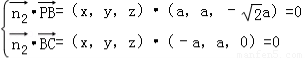
即: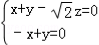 ,取
,取 =1,
=1,
则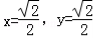 ∴
∴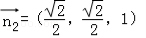 (10分)
(10分)
设平面PAD与平面PBC所成锐二面角的大小为θ,
(Ⅱ)因为求平面PAD与PBC所成锐二面角的大小,如果做出二面角的平面角有一定的困难,可以延长CB与直线DA相交,从而取求解可以.本小题通过建立空间直角坐标系来求解,求出两个平面的法向量,再通过求出法向量的夹角从而得到二面角的大小.
∴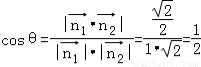 (11分)
(11分)
∴θ=60°,所以平面PAD与平面PBC所成锐二面角的大小为60° (12分)
考点:1.直线与平面的平行关系.2平面与平面的关系.3.三角形的中位线的知识.4.空间直角坐标系的公式.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=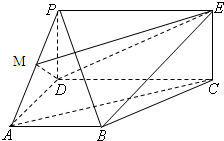 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=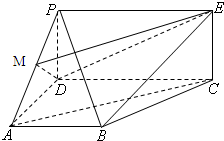
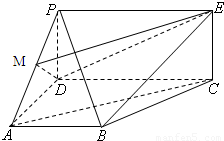 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=a,PD=
CD=a,PD=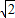 a.
a.