题目内容
 如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=| 1 |
| 2 |
| 2 |
(Ⅰ)若M为PA的中点,求证AC∥平面MDE;
(Ⅱ)求三棱锥A-MDE的体积.
分析:(Ⅰ)若M为PA的中点,链接PC,交DE于点N,可得MN为三角形PAC的中位线,故有MN∥AC.再根据直线和平面平行的判定定理证得 AC∥平面MDE.
(Ⅱ)由题意可得CD⊥平面PAD,再由CE平行于平面PAD可得,点E到平面PAD的距离等于CD.再根据三棱锥A-MDE的体积VA-MDE=VE-DAM=
•SADM•CD,运算求得结果.
(Ⅱ)由题意可得CD⊥平面PAD,再由CE平行于平面PAD可得,点E到平面PAD的距离等于CD.再根据三棱锥A-MDE的体积VA-MDE=VE-DAM=
| 1 |
| 3 |
解答: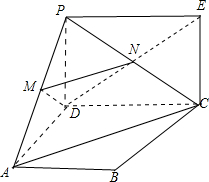 证明:(Ⅰ)若M为PA的中点,链接PC,交DE于点N,
证明:(Ⅰ)若M为PA的中点,链接PC,交DE于点N,
由四边形PDCE为矩形,可得N为PC的中点,
故MN为三角形PAC的中位线,故有MN∥AC.
而MN?平面MDE,AC不在平面MDE内,故有AC∥平面MDE.
(Ⅱ)由于平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,
AB=AD=
CD=a,PD=
a,故有CD⊥平面PAD.
再由CE平行于平面PAD可得,点E到平面PAD的距离等于CD.
三棱锥A-MDE的体积VA-MDE=VE-DAM=
•SADM•CD
=
•(
•SPAD)•CD=
•(
•
a•
a)•2a=
•a3.
 证明:(Ⅰ)若M为PA的中点,链接PC,交DE于点N,
证明:(Ⅰ)若M为PA的中点,链接PC,交DE于点N,由四边形PDCE为矩形,可得N为PC的中点,
故MN为三角形PAC的中位线,故有MN∥AC.
而MN?平面MDE,AC不在平面MDE内,故有AC∥平面MDE.
(Ⅱ)由于平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,
AB=AD=
| 1 |
| 2 |
| 2 |
再由CE平行于平面PAD可得,点E到平面PAD的距离等于CD.
三棱锥A-MDE的体积VA-MDE=VE-DAM=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 6 |
点评:本题主要考查直线和平面平行的判定定理的应用,用等体积法求棱锥的体积,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
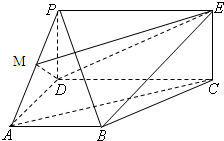 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=

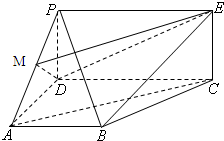
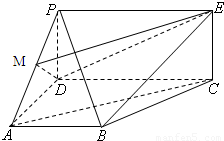 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=a,PD=
CD=a,PD=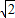 a.
a.