题目内容
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
CD=a,PD=
a.
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求平面PAD与PBC所成锐二面角的大小.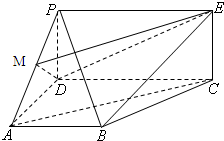
| 1 |
| 2 |
| 2 |
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求平面PAD与PBC所成锐二面角的大小.

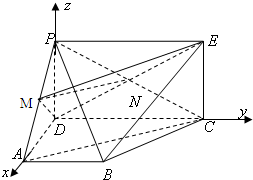
(1)证明:连接PC,交DE与N,连接MN,
在△PAC中,∵M,N分别为两腰PA,PC的中点
∴MN∥AC,…(2分)
又AC?面MDE,MN?面MDE,
所以 AC∥平面MDE.…(4分)
(2)以D为空间坐标系的原点,分别以 DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系,
则P(0,0,
| 2 |
所以
| PB |
| 2 |
| BC |
设平面PAD的单位法向量为
| n1 |
| n1 |
设面PBC的法向量
| n2 |
则有
|
即:
|
则x=
| ||
| 2 |
| ||
| 2 |
| n2 |
| ||
| 2 |
| ||
| 2 |
设平面PAD与平面PBC所成锐二面角的大小为θ,
∴cosθ=
|
| ||||
|
|
| ||||
1•
|
| 1 |
| 2 |
∴θ=60°,
所以平面PAD与平面PBC所成锐二面角的大小为60°…(12分)

练习册系列答案
相关题目
 如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=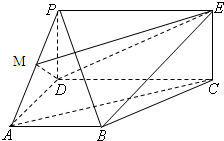 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=

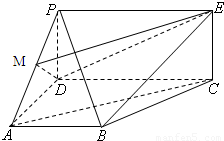 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=a,PD=
CD=a,PD=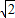 a.
a.