题目内容
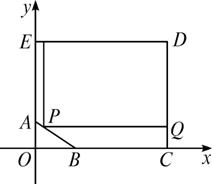
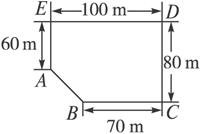
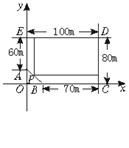
如图,某房地产公司要在荒地ABCDE上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发面积最大,并求出最大面积.(已知BC=210 m,CD=240 m,DE=300 m,EA=180 m)
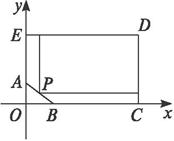
思路解析：这是一道规划问题,问题可以转化为在线段AB上求一点,使矩形面积最大的问题.求出直线AB的方程,求解P点坐标是问题的切入点. 解：如图,以BC所在直线为x轴,AE所在直线为y轴建立平面直角坐标系xOy,则A(0,60),B(90,0).AB所在的直线方程为 ∴可设P(x,60- 开发面积为S=(300-x)(240-y)=(300-x)·［240-(60- ∴S=- 当x=- 答:矩形顶点P距AE15 m,距BC 50 m时面积最大,最大面积为54 150 m2.
+
=1,即y=60-
x.
x).
x)］.
x2+20x+54 000(0＜x＜90
.
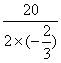=15且y=50时,S取最大值54 150 m2.
练习册系列答案
作业优化系列答案
精练与提高系列答案
30分钟狂练系列答案
赢在课堂课时作业系列答案
赢在课堂周测单元期中期末系列答案
单元同步训练测试题系列答案
励耘书业励耘新同步系列答案
一线课堂学业测评系列答案
相关题目
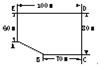某房地产公司要在荒地ABCDE（如图）上划出一块长方形地面（不改变方位）建造一幢八层的公寓楼，问如何设计才能使公寓占地面积最大？并求出最大面积．（精确到1 m2）
某房地产公司要在荒地ABCDE（如图所示）上划出一块长方形地面建造一幢公寓，问：如何设计才能使公寓占地面积最大？求出最大面积（尺寸单位：m）．
m2)．