Question

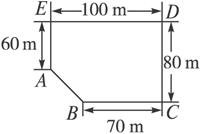
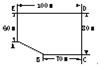某房地产公司要在荒地ABCDE（如图）上划出一块长方形地面（不改变方位）建造一幢八层的公寓楼，问如何设计才能使公寓占地面积最大？并求出最大面积．（精确到1 m²）

Answer 1

分析：根据图形在线段AB上任取一点P，分别向CD、DE作垂线划得一块长方形土地，然后建立直角坐标系，求得直线AB的方程为

x

30

+

y

20

=1．从而设点P坐标为（x，20-

2

3

x），建立长方形面积模型，再根据函数模型求最值．

解答：解：如下图，在线段AB上任取一点P，
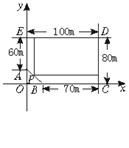
分别向CD、DE作垂线划得一块长方形土地，建立如下图所示的直角坐标系，则AB的方程为

x

30

+

y

20

=1．设P（x，20-

2

3

x），则长方形面积S=（100-x）[80-（20-

2

3

x）]（0≤x≤30）．
化简得S=-

2

3

x²+

20

3

x+6000（0≤x≤30）．
配方，易得x=5，y=

50

3

时，S最大，其最大值为6017m²．

点评：本题主要考查平面图形面积的解法，主要涉及如何建立直角坐标系，求直线的方程，建立函数模型等，属中档题．