题目内容
14．若关于x的方程ax2-1=lnx有两解，求实数a的取值范围．分析 由题意可得a=$\frac{1+lnx}{{x}^{2}}$有两个不等的实根．求出f（x）=$\frac{1+lnx}{{x}^{2}}$的导数和单调区间，最大值，画出图象，通过图象即可得到两个交点的情况，求得a的范围．
解答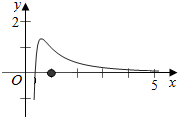 
解：由ax2-1=lnx，可得a=$\frac{1+lnx}{{x}^{2}}$，x＞0．
由题意可得方程a=$\frac{1+lnx}{{x}^{2}}$有两个不等的实根．
f（x）=$\frac{1+lnx}{{x}^{2}}$的导数为f′（x）=$\frac{-1-2lnx}{{x}^{3}}$，
当x＞$\frac{1}{\sqrt{e}}$时，f′（x）＜0，f（x）递减；
当0＜x＜$\frac{1}{\sqrt{e}}$时，f′（x）＞0，f（x）递增．
即有x=$\frac{1}{\sqrt{e}}$处f（x）取得最大值$\frac{e}{2}$．
画出函数f（x）=$\frac{1+lnx}{{x}^{2}}$的图象，
由图象可得当0＜a＜$\frac{e}{2}$时，
直线y=a和函数y=f（x）的图象有两个交点．
则实数a的范围是（0，$\frac{e}{2}$）．
点评 本题考查函数的性质和运用，主要考查函数的零点的判断，注意运用函数方程的转化思想和数形结合的思想方法，属于中档题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
4．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
（1）根据上面的数据判断，y=ax+b与y=$\frac{c}{x}$+d哪一个适宜作为产品销量y关于单价x的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；（计算结果保留两位小数）
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
| 单价x（元） | 0.25 | 0.5 | 1 | 2 | 4 |
| 销量y（件） | 16 | 12 | 5 | 2 | 1 |
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；（计算结果保留两位小数）
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
5．在空间直角坐标系中，A（1，2，3），B（2，2，0），则$\overrightarrow{AB}$=（ ）
| A． | （1，0，-3） | B． | （-1，0，3） | C． | （3，4，3） | D． | （1，0，3） |
19．已知一个平放的棱长为4的三棱锥内有一小球O（重量忽略不计），现从该三棱锥顶端向内注水，小球慢慢上浮，若注入的水的体积是该三棱锥体积的$\frac{7}{8}$时，小球与该三棱锥各侧面均相切（与水面也相切），则球的表面积等于（ ）
| A． | $\frac{7}{6}$π | B． | $\frac{4}{3}$π | C． | $\frac{2}{3}$π | D． | $\frac{1}{2}$π |