题目内容
求下列函数的单调减区间(1)y=lg(x2+4x+2).(2)y=
.
| 1 | ||
|
分析:(1)函数的单调减区间就是真数大于0时的减区间.
(2)函数的减区间就是分母的增区间,且分母不为0.
(2)函数的减区间就是分母的增区间,且分母不为0.
解答:解;(1)y=lg(x2+4x+2)的单调区间,即t=x2+4x+2大于0时的增区间,t=[x-(-2+
)][x-(-2-
)],
由二次函数t=x2+4x+2的图象知,在区间(-2+
,+∞)上,t>0,且t是增函数.
故y=lg(x2+4x+2)的单调增区间为:(-2+
,+∞),
在区间(-∞,-2-
)上,t>0,且t是减函数,故y=lg(x2+4x+2)的单调减区间为
(-∞,-2-
)
(2)∵y=
,
∴函数的减区间就是函数 g=
-3≠0 时的增区间,
又函数 g=
-3在它的定义域[0,+∞)内是增函数,
∴x≥0且 x≠9,
∴函数y的单调减区间为:[0,9)∪(9,+∞).
| 2 |
| 2 |
由二次函数t=x2+4x+2的图象知,在区间(-2+
| 2 |
故y=lg(x2+4x+2)的单调增区间为:(-2+
| 2 |
在区间(-∞,-2-
| 2 |
(-∞,-2-
| 2 |
(2)∵y=
| 1 | ||
|
∴函数的减区间就是函数 g=
| x |
又函数 g=
| x |
∴x≥0且 x≠9,
∴函数y的单调减区间为:[0,9)∪(9,+∞).
点评:本题考查函数的单调性与函数的特殊点.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
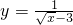 .
.