题目内容
已知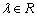 ,函数
,函数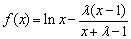 ,其中
,其中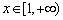 .
.
(Ⅰ)当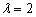 时,求
时,求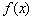 的最小值;
的最小值;
(Ⅱ)在函数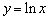 的图像上取点
的图像上取点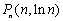
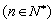 ,记线段PnPn+1的斜率为kn ,
,记线段PnPn+1的斜率为kn ,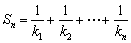 .对任意正整数n,试证明:
.对任意正整数n,试证明:
(ⅰ)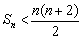 ;
;
(Ⅰ)0;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅱ)利用两点的连线的斜率公式得出kn,再利用(Ⅰ)的结论对Sn放缩即可得出结论.
(Ⅰ)当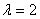 时,
时,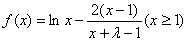 ,利用导数求函数的最小值;(Ⅱ)依题意,
,利用导数求函数的最小值;(Ⅱ)依题意,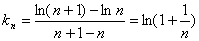 (ⅰ)由(Ⅰ)可知,若取
(ⅰ)由(Ⅰ)可知,若取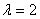 ,则当
,则当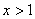 时
时 ,即
,即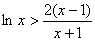
于是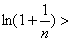
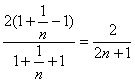 ,即知
,即知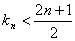 ,所以
,所以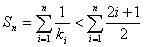 化简即可得到结果.
化简即可得到结果.
(ⅱ)取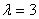 ,
,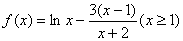 ,求导可得
,求导可得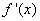
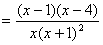 ,所以当
,所以当 时,
时, ,故
,故 在
在 单调递减,所以,当
单调递减,所以,当 时,
时, ,即
,即
由于对任意正整数 ,
, ,于是利用不等式放缩可得
,于是利用不等式放缩可得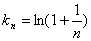
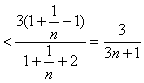 ,即知
,即知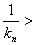
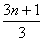 ,即可得到结论.
,即可得到结论.
试题解析:(Ⅰ)当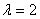 时,
时,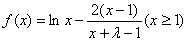 ,求导可得
,求导可得

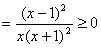
所以 在
在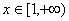 单调递增,故
单调递增,故 的最小值是
的最小值是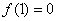 5分
5分
(Ⅱ)依题意,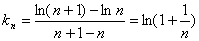 6分
6分
(ⅰ)由(1)可知,若取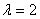 ,则当
,则当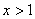 时
时 ,即
,即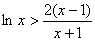
于是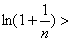
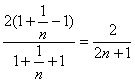 ,即知
,即知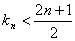
所以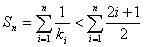
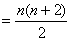 9分
9分
(ⅱ)取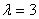 ,
,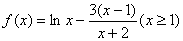 ,求导可得
,求导可得
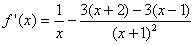
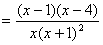
当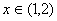 时,
时,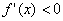 ,故
,故 在
在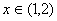 单调递减,
单调递减,
所以,当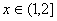 时,
时,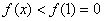 ,即
,即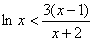 12分
12分
注意到,对任意正整数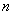 ,
, ,于是
,于是
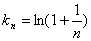
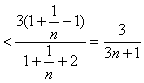 ,即知
,即知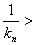
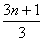
所以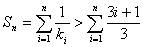
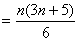 14分.
14分.

练习册系列答案
相关题目

 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围; 时,求证:对大于
时,求证:对大于 的任意正整数
的任意正整数 ,都有
,都有 。
。 则
则 的最大值为 .
的最大值为 . 是真命题,
是真命题, 是假命题,则
是假命题,则 是真命题 (B)
是真命题 (B) 是假命题
是假命题  是真命题 (D)
是真命题 (D) 是真命题
是真命题 满足
满足 ,且
,且 是纯虚数,求
是纯虚数,求 。
。 中,前四项之和为20,最后四项之和为60,前
中,前四项之和为20,最后四项之和为60,前 项之和是100,则项数
项之和是100,则项数 则z=
则z= 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 则
则
 B.
B. C.
C. D.
D.
 ,则复数
,则复数 在复平面内所对应的点在( )
在复平面内所对应的点在( )