题目内容
已知函数
(1)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(2)讨论函数 的单调性;
的单调性;
(3)当 时,求证:对大于
时,求证:对大于 的任意正整数
的任意正整数 ,都有
,都有 。
。
解:(1)∵  ∴
∴ 
 ......1
......1
∵ 函数 在
在
 上为增函数 ∴
上为增函数 ∴ 
 对
对
 恒成立
恒成立

 对
对
 恒成立,即
恒成立,即
 对
对
 恒成立∴
恒成立∴ 
 4分
4分
(2)
 ,
,
当 时,
时, 对
对 恒成立,
恒成立, 的增区间为
的增区间为 ......5
......5
当 时,
时, ,
,
 的增区间为
的增区间为 ,减区间为(
,减区间为( )......6
)......6
(3)当
 时,
时,
 ,
,
 ,故
,故
 在
在
 上为增函数。
上为增函数。
当
 时,令
时,令
 ,则
,则
 ,故
,故
 ......8
......8
∴ 
 ,即
,即

∴ 


【解析】第一问利用 求导数,利用函数
求导数,利用函数 在
在 上为增函数
上为增函数

 对
对
 恒成立
恒成立
来解决
第二问
 ,
,
当 时,
时, 对
对 恒成立,
恒成立, 的增区间为
的增区间为
当 时,
时, ,
,
 的增区间为
的增区间为 ,减区间为(
,减区间为( ).
).
第三问a=1时, ,
,
 ,故
,故 在
在
 上为增函数。
上为增函数。
当n>1时,令
 ,则x>1,故
,则x>1,故

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的分布列是:
的分布列是:

 展开式中含
展开式中含 项的系数等于_________.
项的系数等于_________. 、
、 ,“
,“ ”是“
”是“ ”成立的( )
”成立的( )
 且
且
 若
若
 则
则
 ______.
______.
 则
则 等于( )
等于( ) B.
B. C.
C. D.
D.
 ,
, ,则直线
,则直线 通过( )
通过( )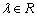 ,函数
,函数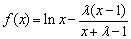 ,其中
,其中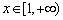 .
.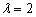 时,求
时,求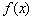 的最小值;
的最小值;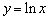 的图像上取点
的图像上取点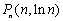
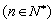 ,记线段PnPn+1的斜率为kn ,
,记线段PnPn+1的斜率为kn ,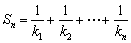 .对任意正整数n,试证明:
.对任意正整数n,试证明: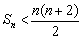 ;
;