题目内容
下列各式：
①|
|=
；
②（
•
）•
=
•（
•
）；
③在任意四边形ABCD中M为AD中点，N为BC中点，则
+
=2
；
④
=（cosa，sina），
=（cosβ，sinβ）且
与
不共线，则（
+
）⊥（
-
）；
其中正确的有（ ）个．
①|
| a |
|
②（
| a |
| b |
| c |
| a |
| b |
| c |
③在任意四边形ABCD中M为AD中点，N为BC中点，则
| AB |
| DC |
| MN |
④
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
其中正确的有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
考点：命题的真假判断与应用,平面向量共线（平行）的坐标表示,平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的模判断①的正误；向量数量积的运算法则判断②的正误；利用平面向量基本定理判断③的正误；向量的数量积判断向量垂直判断④的正误．
解答：
解：对于①，|
|=
=
，所以①正确．
对于②，（
•
）•
，表示与
共线的向量，
•（
•
）表示与
共线的向量，显然②不正确；
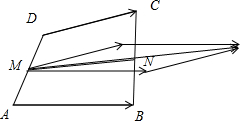
对于③，在任意四边形ABCD中M为AD中点，N为BC中点，如图：则
+
=2
；所以③正确．
④
=（cosα，sinα），
=（cosβ，sinβ）且
与
不共线，则
+
=（cosα+cosβ，sinα+sinβ），
-
═（cosα-cosβ，sinα-sinβ），（
+
）•（
-
）=cos2α-cos2β+sin2α-sin2β=0，（
+
）⊥（
-
）．④正确；
故选：C．
解：对于①，|| a |
|
|
对于②，（
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
对于③，在任意四边形ABCD中M为AD中点，N为BC中点，如图：则
| AB |
| DC |
| MN |
④
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选：C．
点评：本题考查向量的基本运算，向量的数量积以及向量的平行四边形法则的应用，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
| ∫ | 4 2 |
| 1 |
| x |
| A、-2ln2 |
| B、ln 2 |
| C、2 ln 2 |
| D、-ln2 |
设数列{an}，a1=1，前n项和为Sn，若Sn+1=3Sn（n∈N*），则数列{an}的第5项是（ ）
| A、81 | ||
B、
| ||
| C、54 | ||
| D、162 |
阅读下面的程序：
可知程序运行的结果是（ ）
可知程序运行的结果是（ ）
| A、3 | B、3 4 |
| C、3 4 5 | D、3 4 5 6 |
已知命题p：?x∈R，tanx＜1，则（ ）
| A、￢p：?x∈R，tanx＞1 |
| B、￢p：?x∈R，tanx≥1 |
| C、￢p：?x∈R，tanx＞1 |
| D、￢p：?x∈R，tanx≥1 |