题目内容
如果以原点为圆心的圆经过双曲线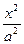 -
-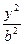 =1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于
=1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于
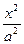 -
-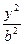 =1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于
=1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于A.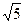 | B.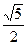 | C. | D.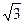 |
C
略

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
题目内容
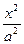 -
-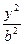 =1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于
=1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于A.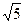 | B.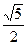 | C. | D.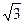 |

 口算能手系列答案
口算能手系列答案