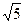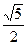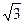题目内容
(本题满分14分)给定椭圆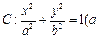 >
>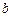 >0
>0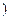 ,称圆心在原点
,称圆心在原点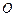 ,半径为
,半径为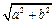 的圆是椭圆
的圆是椭圆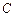 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆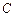 的一个焦点为
的一个焦点为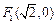 ,其短轴上的一个端点到
,其短轴上的一个端点到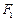 的距离为
的距离为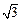 .
.
(1)求椭圆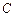 的方程及其“伴随圆”方程;
的方程及其“伴随圆”方程;
(2)若倾斜角为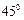 的直线
的直线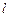 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆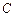 的伴随圆相交于M、N两
的伴随圆相交于M、N两
点,求弦MN的长;
(3)点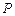 是椭圆
是椭圆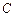 的伴随圆上的一个动点,过点
的伴随圆上的一个动点,过点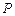 作直线
作直线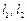 ,使得
,使得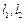 与椭圆
与椭圆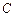 都只有一个公共点,求证:
都只有一个公共点,求证: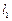 ⊥
⊥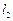 .
.
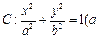 >
>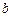 >0
>0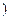 ,称圆心在原点
,称圆心在原点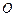 ,半径为
,半径为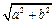 的圆是椭圆
的圆是椭圆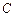 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆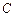 的一个焦点为
的一个焦点为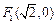 ,其短轴上的一个端点到
,其短轴上的一个端点到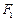 的距离为
的距离为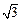 .
.(1)求椭圆
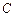 的方程及其“伴随圆”方程;
的方程及其“伴随圆”方程;(2)若倾斜角为
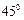 的直线
的直线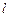 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆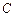 的伴随圆相交于M、N两
的伴随圆相交于M、N两点,求弦MN的长;
(3)点
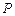 是椭圆
是椭圆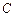 的伴随圆上的一个动点,过点
的伴随圆上的一个动点,过点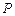 作直线
作直线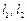 ,使得
,使得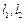 与椭圆
与椭圆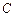 都只有一个公共点,求证:
都只有一个公共点,求证: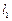 ⊥
⊥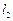 .
.解:(1)因为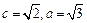 ,所以
,所以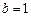 ,所以椭圆的方程为
,所以椭圆的方程为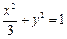 ,
,
伴随圆的方程为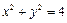 . ……………………………… 4分
. ……………………………… 4分
(2)设直线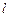 的方程
的方程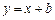 ,由
,由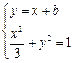 得
得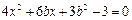
由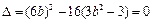 得
得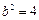 ,圆心到直线
,圆心到直线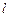 的距离为
的距离为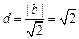
所以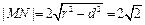 。 ……………………………… 8分
。 ……………………………… 8分
(3)①当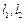 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设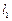 无斜率,
无斜率,
因为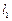 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为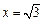 或
或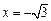 ,
,
当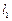 方程为
方程为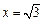 时,此时
时,此时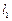 与伴随圆交于点
与伴随圆交于点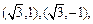
此时经过点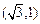 (或
(或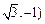 且与椭圆只有一个公共点的另一条直线是
且与椭圆只有一个公共点的另一条直线是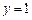 (或
(或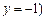 ,即
,即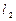 为
为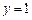 (或
(或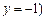 ,显然直线
,显然直线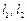 垂直;
垂直;
同理可证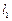 方程为
方程为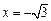 时,直线
时,直线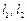 垂直. ……………………………… 10分
垂直. ……………………………… 10分
②当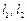 都有斜率时,设点
都有斜率时,设点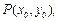 其中
其中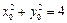 ,
,
设经过点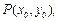 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为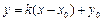 ,
,
由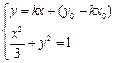 ,消去
,消去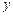 得到
得到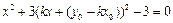 ,
,
即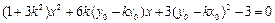 ,
, 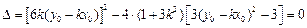 ,
,
经过化简得到: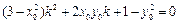 ,
,
因为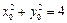 ,所以有
,所以有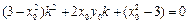 ,
,
设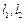 的斜率分别为
的斜率分别为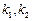 ,因为
,因为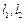 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,
所以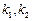 是关于
是关于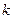 的方程:
的方程: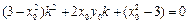 的两个实数根,
的两个实数根,
因而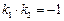 ,即
,即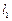 ⊥
⊥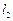 . ……………………………… 14分
. ……………………………… 14分
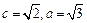 ,所以
,所以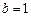 ,所以椭圆的方程为
,所以椭圆的方程为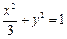 ,
,伴随圆的方程为
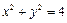 . ……………………………… 4分
. ……………………………… 4分(2)设直线
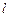 的方程
的方程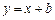 ,由
,由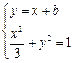 得
得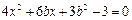
由
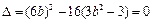 得
得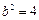 ,圆心到直线
,圆心到直线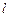 的距离为
的距离为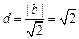
所以
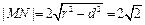 。 ……………………………… 8分
。 ……………………………… 8分(3)①当
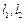 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设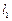 无斜率,
无斜率,因为
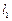 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为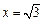 或
或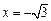 ,
,当
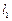 方程为
方程为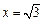 时,此时
时,此时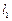 与伴随圆交于点
与伴随圆交于点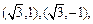
此时经过点
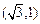 (或
(或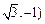 且与椭圆只有一个公共点的另一条直线是
且与椭圆只有一个公共点的另一条直线是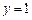 (或
(或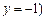 ,即
,即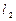 为
为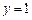 (或
(或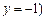 ,显然直线
,显然直线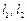 垂直;
垂直; 同理可证
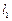 方程为
方程为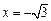 时,直线
时,直线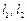 垂直. ……………………………… 10分
垂直. ……………………………… 10分②当
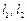 都有斜率时,设点
都有斜率时,设点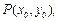 其中
其中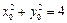 ,
,设经过点
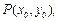 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为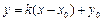 ,
,由
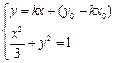 ,消去
,消去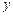 得到
得到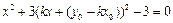 ,
,即
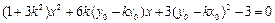 ,
, 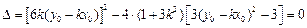 ,
,经过化简得到:
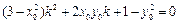 ,
, 因为
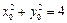 ,所以有
,所以有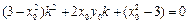 ,
,设
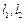 的斜率分别为
的斜率分别为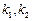 ,因为
,因为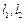 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,所以
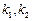 是关于
是关于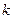 的方程:
的方程: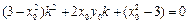 的两个实数根,
的两个实数根,因而
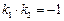 ,即
,即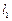 ⊥
⊥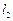 . ……………………………… 14分
. ……………………………… 14分略

练习册系列答案
相关题目
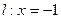 相切。
相切。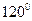 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线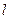 上的射影是
上的射影是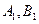 。求梯形
。求梯形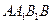 的面积;
的面积;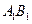 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。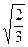 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段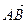 的比为2.
的比为2.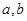 的等差中项是
的等差中项是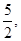 一个等比中项是
一个等比中项是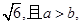 则双曲线
则双曲线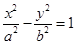 的离心率
的离心率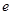 等于
等于 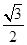
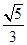
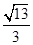
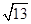

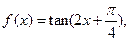 ,
,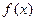 的定义域与最小正周期;
的定义域与最小正周期;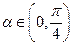 ,若
,若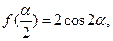 求
求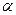 的大小.
的大小.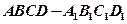 中,
中,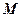 为
为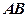 的中点,P是平面
的中点,P是平面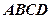 内的动点,且满足条件
内的动点,且满足条件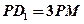 ,则动点P在平面
,则动点P在平面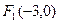 、
、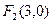 为焦点,渐近线方程为
为焦点,渐近线方程为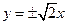 的双曲线的标准方程是 ▲ .
的双曲线的标准方程是 ▲ .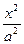 -
-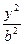 =1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于
=1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于