题目内容
设命题 在
在 内单调递增,命题
内单调递增,命题 ,则命题
,则命题 是命题
是命题 的: ( )
的: ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
C
解析试题分析:若有 在
在 内单调递增,则有
内单调递增,则有 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立,所以
上恒成立,所以 恒成立,所以
恒成立,所以 ,所以命题
,所以命题 是命题
是命题 的充分必要条件.
的充分必要条件.
考点:本小题主要考查函数的导数与单调性的关系、充分必要条件和恒成立问题,考查了学生运算数学知识解决问题的能力.
点评:利用导数研究函数的单调性,大多数情况下归结为对含有参数的一元二次不等式的解集的讨论,有时也转化为恒成立问题进而转化为求最值来完成.

练习册系列答案
相关题目
下列命题中,真命题是.
A.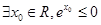 | B.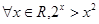 |
C.a+b=0的充要条件是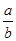 =-1 =-1 | D.a>1,b>1是ab>1的充分条件 |
若m∈R,则“m=1”是“∣m∣=1”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题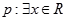 ,使
,使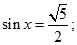 命题
命题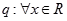 ,都有
,都有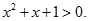
给出下列结论:① 命题“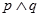 ”是真命题 ② 命题“
”是真命题 ② 命题“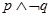 ”是假命题
”是假命题
③ 命题“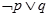 ”是真命题; ④ 命题“
”是真命题; ④ 命题“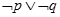 ”是假命题
”是假命题
其中正确的是
| A.② ④ | B.② ③ | C.③ ④ | D.① ② ③ |
已知命题 :
: ,
, ,那么命题
,那么命题 为( )
为( )
A. , , | B. , , |
C. , , | D. , , |
命题“存在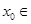 R,
R,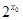
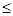 0”的否定是( )
0”的否定是( )
A.不存在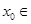 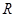 , ,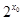 >0 >0 | B.存在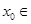 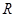 , , 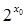 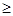 0 0 |
C.对任意的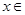 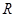 , , 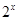 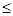 0 0 | D.对任意的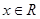 , ,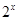 >0 >0 |
若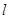 为一条直线,
为一条直线,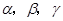 为三个互不重合的平面,给出下面三个命题:
为三个互不重合的平面,给出下面三个命题:
①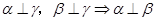 ;②
;②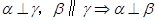 ;③
;③ .其中正确的命题有( )
.其中正确的命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
 是幂函数,则函数
是幂函数,则函数