题目内容
设函数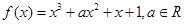 。
。
(Ⅰ)若 时,函数
时,函数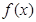 取得极值,求函数
取得极值,求函数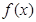 的图像在
的图像在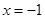 处的切线方程;
处的切线方程;
(Ⅱ)若函数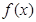 在区间
在区间 内不单调,求实数
内不单调,求实数 的取值范围。
的取值范围。
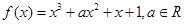 。
。(Ⅰ)若
 时,函数
时,函数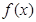 取得极值,求函数
取得极值,求函数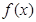 的图像在
的图像在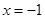 处的切线方程;
处的切线方程;(Ⅱ)若函数
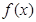 在区间
在区间 内不单调,求实数
内不单调,求实数 的取值范围。
的取值范围。(Ⅰ)切线方程为 ;(Ⅱ)
;(Ⅱ) .
.
 ;(Ⅱ)
;(Ⅱ) .
.试题分析:(Ⅰ)求函数
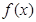 的图像在
的图像在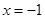 处的切线方程,首先求出函数
处的切线方程,首先求出函数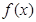 的解析式,而已知若
的解析式,而已知若 时,函数
时,函数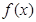 取得极值,因此先求出数
取得极值,因此先求出数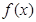 的导函数,令导函数在
的导函数,令导函数在 处的值为
处的值为 ,求出
,求出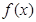 的解析式,将
的解析式,将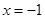 代入
代入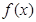 求出切点坐标,将
求出切点坐标,将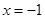 代入导函数求出切线的斜率,利用点斜式求出切线的方程.(Ⅱ)若函数
代入导函数求出切线的斜率,利用点斜式求出切线的方程.(Ⅱ)若函数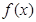 在区间
在区间 内不单调,即函数
内不单调,即函数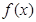 在区间
在区间 有极值,即导函数
有极值,即导函数 在区间
在区间 上有解,令导函数
上有解,令导函数 为
为 ,分离出
,分离出 得
得 ,求出
,求出 在
在 上的范围,从而得实数
上的范围,从而得实数 的取值范围.
的取值范围.试题解析:(Ⅰ)
 由
由 得
得
∴
 当
当 时,
时, 即切点
即切点
 令
令 得
得 ∴切线方程为
∴切线方程为 ;
;(Ⅱ)
 在区间
在区间 内不单调,即
内不单调,即 在
在 有解,所以
有解,所以 ,
, ,由
,由 ,
, ,令
,令 ,
, ,知
,知 在
在 单调递减,在
单调递减,在 ,所以
,所以 ,即
,即 ,
, ,即
,即 ,而当
,而当 时,
时, ∴舍去 综上
∴舍去 综上 

练习册系列答案
相关题目
 )为函数
)为函数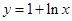 图像上一点,O为坐标原点,记直线OP的斜率
图像上一点,O为坐标原点,记直线OP的斜率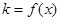 。
。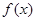 的单调区间;
的单调区间;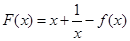 ,求函数
,求函数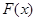 的最小值。
的最小值。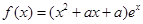 (
(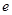 为自然对数的底数)。
为自然对数的底数)。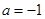 ,求函数
,求函数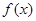 的单调区间;
的单调区间;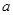 ,使函数
,使函数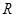 上是单调增函数?若存在,求出
上是单调增函数?若存在,求出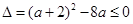
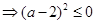 ,又
,又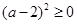 ,
,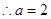
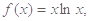
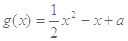 .
.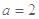 时,求
时,求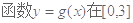 上的值域;
上的值域; 在
在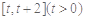 上的最小值;
上的最小值;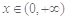 ,都有
,都有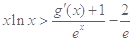 成立
成立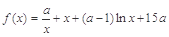 ,
,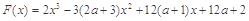 ,其中
,其中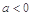 且
且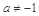 .
. 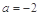 ,求函数
,求函数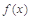 的单调递增区间;
的单调递增区间;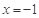 时,函数
时,函数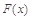 有极值,求函数
有极值,求函数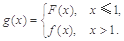 (
(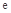 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使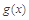 在
在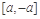 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.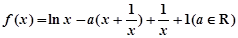 .
.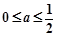 时,试讨论
时,试讨论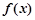 的单调性;
的单调性;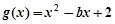 ,当
,当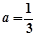 时,若对任意
时,若对任意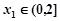 ,存在
,存在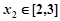 ,使
,使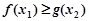 ,求实数
,求实数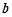 取值范围.
取值范围.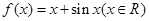 ,且
,且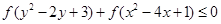 ,则当
,则当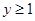 时,
时,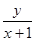 的取值范围是 ( )
的取值范围是 ( )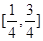
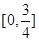
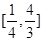
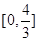
 f’(x)<0,又a=f(log0.53),b=f((
f’(x)<0,又a=f(log0.53),b=f((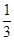 )0.3),c=f(ln3),则( )
)0.3),c=f(ln3),则( )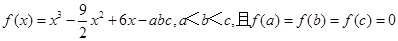 ,现给出如下结论:
,现给出如下结论: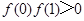 ;②
;②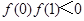 ;③
;③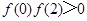 ;④
;④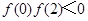 .
.