题目内容
6.已知函数f(x)=|x-2|.(1)求不等式f(x)+x2-4>0的解集;
(2)设g(x)=-|x+7|+3m,若关于x的不等式f(x)<g(x)的解集非空,求实数m的取值范围.
分析 (1)由题意,x-2>4-x2,或x-2<x2-4,分别解不等式,即可求不等式f(x)+x2-4>0的解集;
(2)原不等式等价于|x-2|+|x+7|<3m的解集非空,求出左边的最小值,即可求实数m的取值范围.
解答 解:(1)由题意,x-2>4-x2,或x-2<x2-4,
由x-2>4-x2得x>2或x<-3;由x-2<x2-4得x>2或x<-1,
∴原不等式的解集为{x|x>2或x<-1};
(2)原不等式等价于|x-2|+|x+7|<3m的解集非空,
∵|x-2|+|x+7|≥|x-2-x-7|=9,
∴3m>9,∴m>3.
点评 本题考查不等式的解法,考查绝对值不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(0)=2,则不等式f(x)-2ex<0的解集为( )
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
17.某棱锥的三视图如图所示,则该棱锥的外接球的表面积为( )
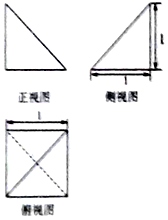

| A. | 3π | B. | 2π | C. | π | D. | 4π |
1.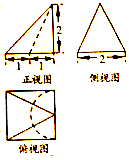 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )
 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )| A. | $\frac{7}{3}$ | B. | $\frac{8-π}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{7-π}{3}$ |
18.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow a+\overrightarrow b}|=1$,则$|{2\overrightarrow a+\overrightarrow b}|$=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 7 | D. | $\sqrt{7}$ |
15.设集合A={x|-x2-x+2<0},B={x|2x-5>0},则集合A与B的关系是( )
| A. | B⊆A | B. | B?A | C. | B∈A | D. | A∈B |