题目内容
2.函数$y=\sqrt{5-{x^2}+4x}$的单调增区间是[-1,2].分析 求出函数的定义域,根据二次函数的性质以及复合函数的单调性求出函数的递增区间即可.
解答 解:由5-x2+4x≥0,解得:-1≤x≤5,
故函数的定义域是[-1,5],
令g(x)=-x2+4x+5,对称轴是;x=2,开口向下,
故g(x)在[-1,2)递增,在(2,5]递减,
根据复合函数的单调性,
得$y=\sqrt{5-{x^2}+4x}$在[-1,2]递增,
故答案为:[-1,2].
点评 本题考查了函数的单调性问题,考查二次函数的性质以及复合函数的单调性,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.执行如图所示的程序框图,若输出的k=8,则输入的k为( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.已知a1,x,y,a2成等差数列,b1,x,y,b2成等比数列.则$\frac{{{{({{a_1}+{a_2}})}^2}}}{{{b_1}{b_2}}}-2$的取值范围是( )
| A. | (0,2] | B. | [-2,0)∪(0,2] | C. | (-∞,-2]∪[2,+∞) | D. | (-∞,-1]∪[1,+∞) |
 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).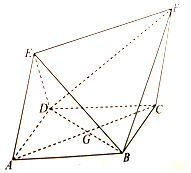 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.