题目内容
14.已知数列{an}的前n项和为Sn,且a1=2,an+1=Sn+2,n∈N*.(1)求数列{an}的通项公式;
(2)若a1,a2分别是等差数列{bn}的第2项和第4项,数列{bn}的前n项和为Tn,求证:1≤$\sum_{i=1}^{n}$$\frac{1}{{T}_{i}}$<2.
分析 (1)利用递推关系及其等比数列的通项公式即可得出;
(2)利用等差数列的通项公式及其“裂项求和”、不等式的性质即可得出.
解答 (1)解:∵an+1=Sn+2,n∈N*.
∴当n≥2时,an=Sn-1+2,可得an+1-an=an,化为an+1=2an.
又a2=a1+2,满足a2=2a1,
∴数列{an}是等比数列,首项为2,公比为2.
∴an=2n.
(2)证明:设等差数列{bn}的公差为d,∵b2=a1=2,b4=a2=4,
∴4-2=2d,解得d=1.
∴bn=b2+(n-2)×1=n.
∴Tn=$\frac{n(n+1)}{2}$,∴$\frac{1}{{T}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.
∴$\sum_{i=1}^{n}$$\frac{1}{{T}_{i}}$=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=$2(1-\frac{1}{n+1})$.
∵1≤$2(1-\frac{1}{n+1})$<2.
∴1≤$\sum_{i=1}^{n}$$\frac{1}{{T}_{i}}$<2.
点评 本题考查了递推关系、等差数列的通项公式及其“裂项求和”、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
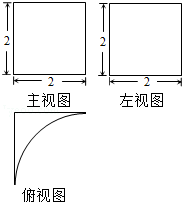 某几何体的三视图如图所示,其中俯视图为半径为2的四分之一个圆弧,则该几何体的体积为8-2π,表面积为16.
某几何体的三视图如图所示,其中俯视图为半径为2的四分之一个圆弧,则该几何体的体积为8-2π,表面积为16.