题目内容
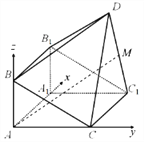
【题目】如图,由三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
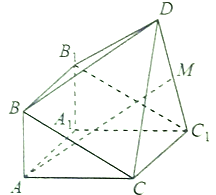
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)不存在这样的点.
【解析】试题分析: (Ⅰ)在直三棱柱![]() 中,由
中,由![]() 平面
平面![]() ,推得
,推得![]() ,
,
由平面![]() 平面
平面![]() ,推得
,推得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,得证.(Ⅱ)如图建立空间直角坐标系
,得证.(Ⅱ)如图建立空间直角坐标系![]() ,写出各点坐标,求出平面
,写出各点坐标,求出平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() , 所以
, 所以![]() 平面
平面![]() .(Ⅲ)设
.(Ⅲ)设![]() ,
, ![]() ,根据线面角公式列出方程,解得
,根据线面角公式列出方程,解得![]() ,可得结论.
,可得结论.
试题解析:(Ⅰ)证明:在直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
,
故![]() ,
,
由平面![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)证明:在直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
,
所以![]() ,
, ![]() ,
,
又![]() ,
,
所以,如图建立空间直角坐标系![]() ,
,
依据已知条件可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由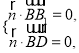 即
即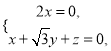
令![]() ,则
,则![]() ,
, ![]() ,于是
,于是![]() ,
,
因为![]() 为
为![]() 中点,所以
中点,所以![]() ,所以
,所以![]() ,
,
由![]() ,可得
,可得![]() ,
,
所以![]() 与平面
与平面![]() 所成角为0,
所成角为0,
即![]() 平面
平面![]() .
.
(Ⅲ)解:由(Ⅱ)可知平面![]() 的法向量为
的法向量为![]() .
.
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
若直线![]() 与平面
与平面![]() 成角为
成角为![]() ,则
,则
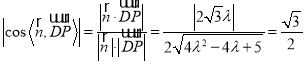 ,
,
解得![]() ,
,
故不存在这样的点.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”、“演讲社”三个金牌社团中抽6人组成社团管理小组,有关数据见下表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求![]() 的值;
的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.