题目内容
【题目】已知圆![]() ,直线
,直线![]() :x=6,圆
:x=6,圆![]() 与
与![]() 轴相交于点
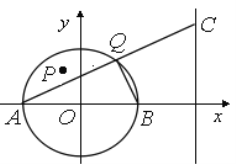
轴相交于点![]() (如图),点P(-1,2)是圆
(如图),点P(-1,2)是圆![]() 内一点,点
内一点,点![]() 为圆
为圆![]() 上任一点(异于点
上任一点(异于点![]() ),直线
),直线![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)若过点P的直线![]() 与圆
与圆![]() 相交所得弦长等于
相交所得弦长等于![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() 或
或![]() (2)-3
(2)-3
【解析】试题分析:(1)由点到直线距离公式可得圆心![]() 到直线的距离
到直线的距离![]() ,设直线
,设直线![]() 的方程为
的方程为![]() , 由
, 由![]() 解得
解得![]() ,又过点P且与
,又过点P且与![]() 轴垂直的直线
轴垂直的直线![]() 显然符合要求,故满足题意的直线
显然符合要求,故满足题意的直线![]() 应为两条;
应为两条;
(2)方法1:联立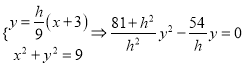 得点
得点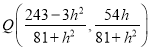
![]() ,问题得证;
,问题得证;
方法2:设点![]() 的坐标为
的坐标为![]() ,分
,分 ![]() ,
, ![]() ,两组情况讨论得证
,两组情况讨论得证
;方法3:设点![]() 的坐标为
的坐标为![]() , 则
, 则![]() ,则由三点A、Q、C三点共线及直线
,则由三点A、Q、C三点共线及直线![]() 的方程得点
的方程得点 ,表示出
,表示出![]() ,可证
,可证![]() 为定值
为定值
试题解析:
(1)因直线![]() 与圆
与圆![]() 相交所得弦长等于
相交所得弦长等于![]() ,所以圆心
,所以圆心![]() 到直线的距离
到直线的距离![]()
设直线![]() 的方程为
的方程为![]() ,即
,即![]()
由![]() 解得
解得![]()
又过点P且与![]() 轴垂直的直线
轴垂直的直线![]() 显然符合要求
显然符合要求
所以直线![]() 的方程是
的方程是![]() 或
或![]()
(2)方法1:设点![]() 的坐标为
的坐标为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由 解得
解得![]()
从而得点
![]()
所以![]()
方法2:设点![]() 的坐标为
的坐标为![]() ,
,
若 ![]() ,则
,则![]()
![]()
![]()
![]()
所以![]()
当![]() 时,同理可得
时,同理可得![]()
所以![]() 为定值
为定值
方法3:设点![]() 的坐标为
的坐标为![]() , 则
, 则![]()
则三点A、Q、C三点共线及直线![]() 的方程得点
的方程得点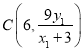
![]()
![]()
![]()

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
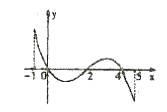
,部分对应值如表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的命题;
的命题;
|
|
|
|
|
|
|
|
|
|
|
|
①函数![]() 的值域为
的值域为![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③如果当![]() 时,
时, ![]() 最大值是
最大值是![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;
;
④当![]() 时,函数
时,函数![]() 最多有4个零点.
最多有4个零点.
其中正确命题的序号是_________.