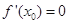题目内容
对于定义域为 的函数
的函数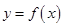 ,如果存在区间
,如果存在区间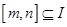 ,同时满足:
,同时满足:
①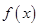 在
在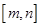 内是单调函数;②当定义域是
内是单调函数;②当定义域是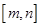 ,
,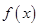 值域也是
值域也是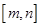 ,则称
,则称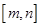 是函数
是函数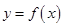
的“好区间”.
(1)设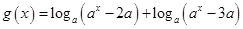 (其中
(其中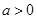 且
且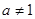 ),判断
),判断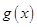 是否存在“好区间”,并
是否存在“好区间”,并
说明理由;
(2)已知函数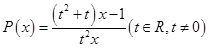 有“好区间”
有“好区间”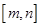 ,当
,当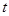 变化时,求
变化时,求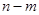 的最大值.
的最大值.
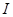 的函数
的函数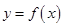 ,如果存在区间
,如果存在区间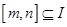 ,同时满足:
,同时满足:①
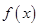 在
在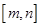 内是单调函数;②当定义域是
内是单调函数;②当定义域是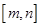 ,
,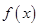 值域也是
值域也是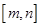 ,则称
,则称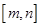 是函数
是函数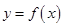
的“好区间”.
(1)设
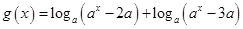 (其中
(其中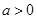 且
且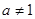 ),判断
),判断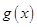 是否存在“好区间”,并
是否存在“好区间”,并说明理由;
(2)已知函数
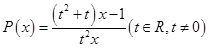 有“好区间”
有“好区间”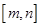 ,当
,当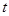 变化时,求
变化时,求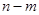 的最大值.
的最大值.(1)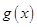 不存在“好区间”;(2)
不存在“好区间”;(2)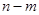 的最大值为
的最大值为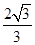 .
.
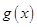 不存在“好区间”;(2)
不存在“好区间”;(2)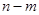 的最大值为
的最大值为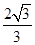 .
.试题分析:(1)先求出
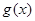 的定义域.可知要对
的定义域.可知要对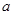 分情况讨论,当
分情况讨论,当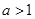 时,定义域
时,定义域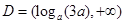 ,
,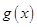 在
在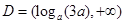 内是增函数;当
内是增函数;当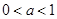 时,定义域
时,定义域 ,
,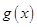 在
在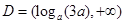 内还是增函数.从而得出
内还是增函数.从而得出 ,即方程
,即方程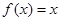 在定义域
在定义域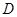 内有两个不等的实数根,即
内有两个不等的实数根,即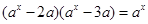 在定义域
在定义域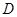 内有两个不等的实数根.再用换元法,设
内有两个不等的实数根.再用换元法,设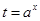 ,则相当于
,则相当于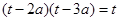 两个不等的实数根,即
两个不等的实数根,即 在
在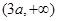 内有两个不等的实数根,通过研究二次函数
内有两个不等的实数根,通过研究二次函数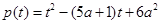 ,发现
,发现 在
在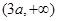 内有两个不等的实数根无解,所以函数
内有两个不等的实数根无解,所以函数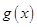 不存在“好区间”;(2)函数
不存在“好区间”;(2)函数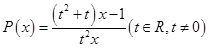 有“好区间”
有“好区间”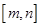 ,由于
,由于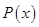 定义域为
定义域为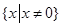 ,
,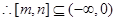 或
或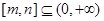 ,易知函数
,易知函数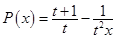 在
在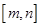 上单调递增,
上单调递增,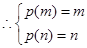 ,所以
,所以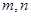 是方程
是方程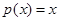 ,即方程
,即方程 有同号的相异实数根,然后再用判别式求出
有同号的相异实数根,然后再用判别式求出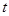 的范围,再用韦达定理用
的范围,再用韦达定理用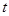 表示出
表示出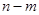 ,结合
,结合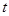 的范围即可求出
的范围即可求出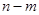 的最大值.
的最大值.试题解析:(1)由
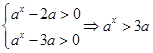 . 2分
. 2分①当
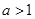 时,
时,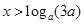 ,此时定义域
,此时定义域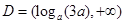 ,
,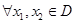 ,
,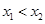 ,
,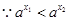 ,
,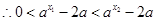 ,
,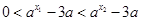 ,
,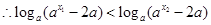 ,
,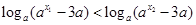 ,
,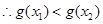 ,
,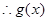 在
在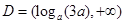 内是增函数; 4分
内是增函数; 4分②当
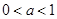 时,
时,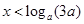 ,此时定义域
,此时定义域 ,
,同理可证
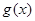 在
在 内是增函数; 6分
内是增函数; 6分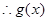 存在“好区间”
存在“好区间”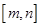
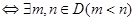 ,
,
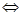 关于
关于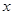 的方程
的方程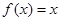 在定义域
在定义域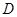 内有两个不等的实数根.
内有两个不等的实数根.即
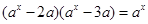 在定义域
在定义域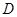 内有两个不等的实数根.(*)
内有两个不等的实数根.(*)设
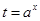 ,则(*)
,则(*)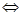
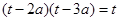 ,
,即
 在
在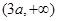 内有两个不等的实数根,
内有两个不等的实数根,设
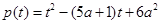 ,则
,则 无解.
无解.所以函数
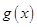 不存在“好区间”. 8分
不存在“好区间”. 8分(2)由题设,函数
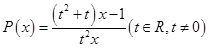 有“好区间”
有“好区间”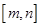 ,
,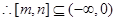 或
或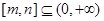 ,函数
,函数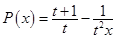 在
在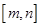 上单调递增,
上单调递增,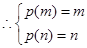 ,所以
,所以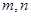 是方程
是方程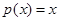 ,即方程
,即方程 有同号的相异实数根. 12分
有同号的相异实数根. 12分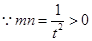 ,
,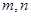 同号,
同号,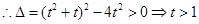 或
或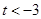 .
.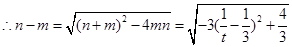 ,
,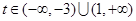 .
.当
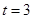 ,
,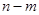 取得最大值
取得最大值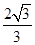 . 16分
. 16分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
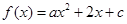 (
(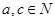 )满足①
)满足①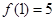 ;②
;②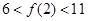
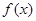 的解析式;
的解析式;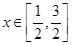 ,都有
,都有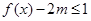 成立,求实数
成立,求实数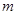 的取值范围.
的取值范围.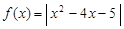 .
.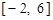 上画出函数
上画出函数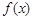 的图象 ;
的图象 ;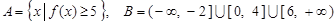 . 试判断集合
. 试判断集合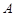 和
和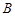 之间
之间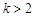 时,求证:在区间
时,求证:在区间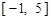 上,
上,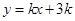 的图象位于函数
的图象位于函数
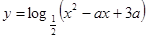 在
在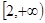 上为减函数,则实数
上为减函数,则实数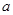 的取值范围是 .
的取值范围是 .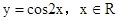
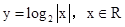 且x≠0
且x≠0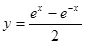 , x
, x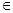 R
R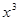 +1, x
+1, x 的最大值为( )
的最大值为( )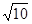
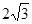
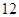
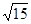
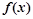 是定义在R上的奇函数,且当x
是定义在R上的奇函数,且当x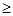 0时,
0时,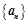 是等差数列,且
是等差数列,且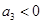 ,则
,则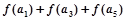 的值 ( )
的值 ( ) 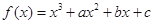 ,下列结论中错误的是( )
,下列结论中错误的是( )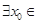 R,
R,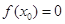
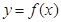 的图像是中心对称图形
的图像是中心对称图形 是
是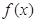 的极小值点,则
的极小值点,则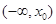 上单调递减
上单调递减