题目内容
【题目】设抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() ,以
,以![]() 为圆心的圆
为圆心的圆![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 的纵坐标为
的纵坐标为![]() ,
,![]() 是圆
是圆![]() 与
与![]() 轴的不同于
轴的不同于![]() 的一个交点.
的一个交点.
(1)求抛物线![]() 与圆
与圆![]() 的方程;
的方程;
(2)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
【答案】(1)![]() :
:![]() ,
,![]() :
:![]() ;(2)
;(2)![]() .
.
【解析】
(1)由抛物线的定义,结合![]() ,确定
,确定![]() 的坐标,根据
的坐标,根据![]() 是线段
是线段![]() 垂直平分线上的点,建立方程,即可求抛物线
垂直平分线上的点,建立方程,即可求抛物线![]() 与圆
与圆![]() 的方程;
的方程;
(2)求出过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 的方程,与抛物线方程联立,求出
的方程,与抛物线方程联立,求出![]() ,
,![]() 的坐标,进而求出
的坐标,进而求出![]() 和
和![]() 到直线
到直线![]() 的距离,即可求
的距离,即可求![]() 的面积.
的面积.
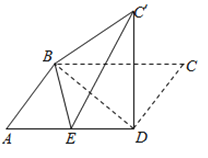
(1)如图: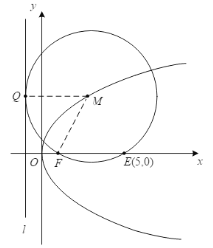
由抛物线的定义知,圆![]() 经过焦点
经过焦点![]() ,
,![]() ,
,
点![]() 的纵坐标为
的纵坐标为![]() ,又
,又![]() ,则
,则![]() ,
,![]() ,
,
由题意,![]() 是线段
是线段![]() 的垂直平分线上的点,又
的垂直平分线上的点,又![]() ,
,
故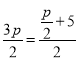 ,解得
,解得![]() ,则
,则![]() ,
,![]() ,圆
,圆![]() 的半径
的半径![]() ,
,
故抛物线![]() :
:![]() ,圆
,圆![]() :
:![]() ;
;
(2)由(1)可知![]() ,直线
,直线![]() :
:![]() ,由
,由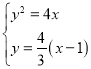 ,解得
,解得![]() 或
或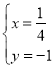 ,
,
如图:

设![]() ,
,![]() ,则
,则![]() ,
,![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() 的面积
的面积![]() .
.

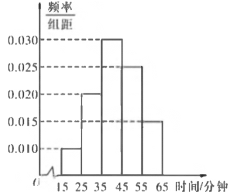
【题目】某学校为了了解该校某年级学生的阅读量(分钟),随机抽取了n名学生,调查他们一天的阅读时间,统计结果下图表所示:
组号 | 分组 | 男生 人数 | 男生人数占本 组人数的频率 | 频率分布直方图 |
第1组 |
| 5 | 0.5 |
|
第2组 |
| 18 | 0.9 | |
第3组 |
| 24 | 0.8 | |
第4组 |
|
| 0.4 | |
第5组 |
| 3 | 0.2 |
(1)求出![]() 与
与![]() 的值;
的值;
(2)—天的阅时间不少于35分钟称为“喜好阅读者”.根据以上数据,完成下面的![]() 列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
喜好阅读者 | 非喜好阅读者 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: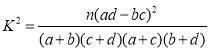 (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】2019年电商“双十一”大战即将开始.某电商为了尽快占领市场,抢占今年“双十一”的先机,对成都地区年龄在15到75岁的人群“是否网上购物”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用网上购物的人数如下所示:(年龄单位:岁)
年龄段 |
|
|
|
|
|
|
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
购物人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | 总计 | |
使用网上购物 | |||
不使用网上购物 | |||
总计 |
(2)若从年龄在![]() 的样本中随机选取2人进行座谈,求选中的2人中恰好有1人“使用网上购物”的概率.
的样本中随机选取2人进行座谈,求选中的2人中恰好有1人“使用网上购物”的概率.
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: .
.