题目内容
【题目】已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点,沿
的中点,沿![]() 将
将![]() 翻折到
翻折到![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
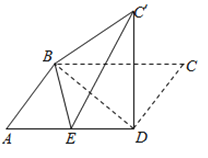
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)首先证出![]() ,再利用面面垂直的性质定理即可证出.
,再利用面面垂直的性质定理即可证出.
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,求出平面
,求出平面![]() 的一个法向量,平面
的一个法向量,平面![]() 的一个法向量,利用空间向量的数量积即可求解.
的一个法向量,利用空间向量的数量积即可求解.
(1)由题意可知![]() ,
,![]() ,
,![]() ,
,
即![]() ,故
,故![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,且
,且![]() ,
,
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴
轴
建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
由于![]() 是线段
是线段![]() 的中点,所以
的中点,所以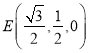 在平面
在平面![]() 中,
中,
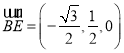 ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则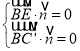 ,即
,即 ,
,
令![]() ,得
,得![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
而平面![]() 的一个法向量为
的一个法向量为![]() .
.
故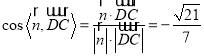 ,易知二面角
,易知二面角![]() 的平面角为锐角,
的平面角为锐角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】10月1日,某品牌的两款最新手机(记为![]() 型号,
型号,![]() 型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
手机店 |
|
|
|
|
|
| 6 | 6 | 13 | 8 | 11 |
| 12 | 9 | 13 | 6 | 4 |
(Ⅰ)若在10月1日当天,从![]() ,
,![]() 这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为
这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为![]() 型号手机的概率;
型号手机的概率;
(Ⅱ)现从这5个手机店中任选3个举行促销活动,用![]() 型号手机销量超过
型号手机销量超过![]() 型号手机销量的手机店的个数,求随机变量
型号手机销量的手机店的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)经测算,![]() 型号手机的销售成本
型号手机的销售成本![]() (百元)与销量(部)满足关系
(百元)与销量(部)满足关系![]() .若表中
.若表中![]() 型号手机销量的方差
型号手机销量的方差![]() ,试给出表中5个手机店的
,试给出表中5个手机店的![]() 型号手机销售成本的方差
型号手机销售成本的方差![]() 的值.(用
的值.(用![]() 表示,结论不要求证明)
表示,结论不要求证明)
【题目】十三届全国人大二次会议于2019年3月5日在京召开为了了解某校大学生对两会的关注程度,学校媒体在开幕后的第二天,从全校学生中随机抽取了180人,对是否收看2019年两会开幕会情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 80 | 40 |
女生 | 30 | 30 |
(1)根据上表说明,在犯错误的概率不超过1%的前提下,能否认为该校大学生收看开幕会与性别有关?(计算结果精确到0.001)
(2)现从随机抽取的学生中,采用按性别分层抽样的方法选取6人,来参加2019年两会的志愿者宣传活动,若从这6人中随机选取2人到各班级宣传介绍,求恰好选到一名男生和一名女生的概率. 附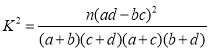 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |