题目内容
8.已知函数f(x)=asinωx+bcosωx(ω>0)的图象如图所示,则f(0)+f(1)+f(2)+f(3)+…+f(2016)=0.
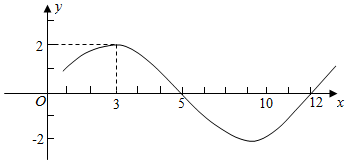
分析 由图象可得ab的方程以及ω的值,解方程可得解析式,由函数的周期性可得.
解答 解:由题意和图象可得a2+b2=4,$\frac{2π}{ω}$=2(12-6),解得ω=$\frac{π}{6}$,
由图象过点(3,2)可得asin$\frac{π}{2}$+bcos$\frac{π}{2}$=2,解得a=2,故b=0,
故函数f(x)=asinωx+bcosωx=2sin$\frac{π}{6}$x,
∴f(0)+f(1)+f(2)+f(3)+…+f(12)=0,
∴f(0)+f(1)+f(2)+f(3)+…+f(2016)=168×0=0,
故答案为:0.
点评 本题考查三角函数的图象和解析式,涉及函数的周期性,属基础题.

练习册系列答案
相关题目
16.已知sin(α+$\frac{π}{6}$)+cosα=$\frac{4}{5}$$\sqrt{3}$,则cos(2α+$\frac{2π}{3}$)的值为( )
| A. | -$\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | $\frac{9}{25}$ | D. | -$\frac{9}{25}$ |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=l(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF2|=$\frac{5}{3}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=l(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF2|=$\frac{5}{3}$.