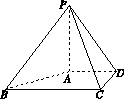
题目内容
已知直三棱柱 中,
中, ,
,
 是
是 中点,
中点,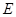 是
是 中点.
中点.
(1)求三棱柱 的体积;
的体积;
(2)求证: ;
;
(3)求证: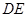 ∥面
∥面 .
.
(1)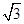 ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.
解析试题分析:(1)这是一个直三棱柱,直接由体积计算公式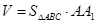 即可求解;(2)要证
即可求解;(2)要证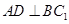 ,只须证明
,只须证明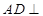 面
面 ,注意到面
,注意到面 与底面
与底面 垂直且交线为
垂直且交线为 ,而依题意又有
,而依题意又有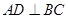 ,由面面垂直的性质可得
,由面面垂直的性质可得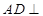 面
面 ,问题得证;(3)要证
,问题得证;(3)要证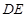 ∥面
∥面 ,有两种思路:一是在平面
,有两种思路:一是在平面 内找一条直线与
内找一条直线与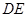 平行,这时只须取
平行,这时只须取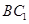 的中点
的中点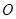 ,连接
,连接 ,证明四边形
,证明四边形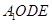 为平行四边形即可;二是先证经过直线
为平行四边形即可;二是先证经过直线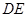 的一个平面与面
的一个平面与面 平行,这时可取
平行,这时可取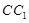 中点
中点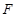 ,连结
,连结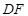 ,
,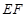 ,先证明面
,先证明面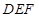 ∥面
∥面 ,再由面面平行的性质即可证明
,再由面面平行的性质即可证明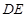 ∥面
∥面 .
.
试题解析:(1) 3分
3分
(2)∵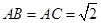 ,∴
,∴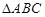 为等腰三角形
为等腰三角形
∵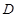 为
为 中点,∴
中点,∴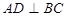 -4分
-4分
∵ 为直棱柱,∴面
为直棱柱,∴面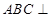 面
面 5分
5分
∵面 面
面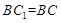 ,
,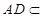 面
面
∴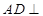 面
面 6分
6分
∴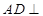
 7分
7分
(3)取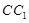 中点
中点 ,连结
,连结 ,
, 8分
8分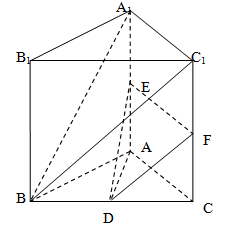
∵ 分别为
分别为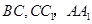 的中点
的中点
∴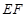 ∥
∥ ,
,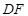 ∥
∥ , 9分
, 9分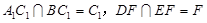
∴面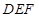 ∥面
∥面 11分
11分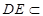 面
面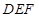

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 中,平面
中,平面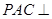 平面
平面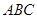 ,
, 是边长为2的正三角形,
是边长为2的正三角形,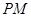 ∥
∥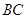 ,且
,且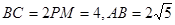 .
.
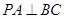 ;
;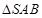 ,
,  为底面圆周上一点.
为底面圆周上一点.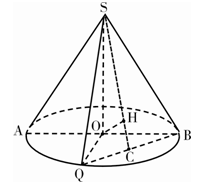
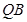 的中点为
的中点为 ,
,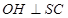 ,求证
,求证 平面
平面 ;
;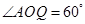 ,
,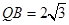 ,求此圆锥的全面积.
,求此圆锥的全面积.
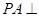 平面ABCD,E,F是AC,PC的中点.
平面ABCD,E,F是AC,PC的中点.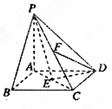
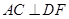 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.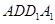 和三棱锥
和三棱锥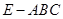 组合而成,点
组合而成,点 、
、 、
、 在圆
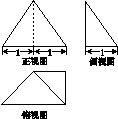
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中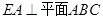 ,
,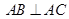 ,
,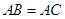 ,
,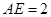 .
.
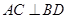 ;
;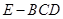 的体积.
的体积.
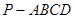 中,
中,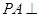 平面
平面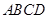 ,底面
,底面 是平行四边形,
是平行四边形,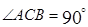 ,
,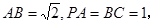
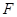 是
是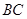 的中点
的中点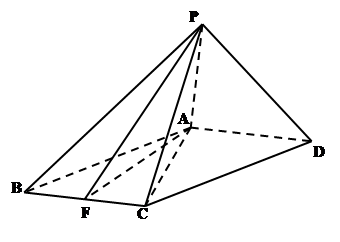
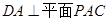
 上确定一点
上确定一点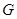 ,使
,使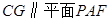 ,求三棱锥
,求三棱锥 的体积.
的体积.