题目内容
8.已知sin($\frac{π}{2}$-θ)-cos(π+θ)=3sin(2π-θ),求sinθcosθ+cos2θ.分析 由诱导公式得到$sinθ=\frac{2}{3}cosθ$,利用同角三角函数关系式求出$co{s}^{2}θ=\frac{9}{13}$,sin2θ=$\frac{4}{13}$,由此能求出sinθcosθ+cos2θ.
解答 解:∵sin($\frac{π}{2}$-θ)-cos(π+θ)=3sin(2π-θ),
∴cosθ+cosθ=3sinθ,
∴$sinθ=\frac{2}{3}cosθ$,
∴cos2θ+sin2θ=$co{s}^{2}θ+\frac{4}{9}co{s}^{2}θ$=1,
解得$co{s}^{2}θ=\frac{9}{13}$,sin2θ=$\frac{4}{13}$,
∴sinθcosθ+cos2θ=$\sqrt{si{n}^{2}θco{s}^{2}θ}$+cos2θ
=$\sqrt{\frac{4}{13}×\frac{9}{13}}+\frac{9}{13}$=$\frac{6}{13}+\frac{9}{13}$=$\frac{15}{13}$.
点评 本题考查三角函数值化简求值,是中档题,解题时要认真审题,注意诱导公式、同角三角函数关系式的合理运用.

练习册系列答案
相关题目
3.非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\sqrt{3}$|$\overrightarrow{a}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则向量$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$-$\overrightarrow{a}$夹角的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
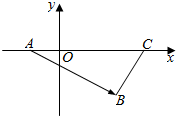 如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.
如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.